Calcule a integral: ∫ (2x^4 + 3x^3 + 3x + 2) / (x(x^2 + 1)^2) dx
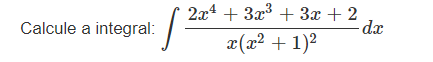
Understand the Problem
La pregunta está pidiendo calcular una integral definida que involucra un polinomio en el numerador y una función cuadrática en el denominador.
Answer
La integral es $$ 2 \ln |x| + B \tan^{-1}(x) + \frac{D}{2(x^2 + 1)} + C $$
Answer for screen readers
La integral es
$$ 2 \ln |x| + B \tan^{-1}(x) + \frac{D}{2(x^2 + 1)} + C $$
Steps to Solve
- Descomposición en fracciones parciales
Primero, descompondremos la fracción en fracciones parciales. La expresión es:
$$ \frac{2x^4 + 3x^3 + 3x + 2}{x(x^2 + 1)^2} $$
Podemos expresar esto como:
$$ \frac{A}{x} + \frac{Bx + C}{x^2 + 1} + \frac{Dx + E}{(x^2 + 1)^2} $$
Donde $A$, $B$, $C$, $D$, y $E$ son constantes que debemos determinar.
- Igualar los numeradores
Multiplicamos ambos lados por el denominador (x(x^2 + 1)^2) y igualamos los numeradores:
$$ 2x^4 + 3x^3 + 3x + 2 = A(x^2 + 1)^2 + (Bx + C)x(x^2 + 1) + (Dx + E)x $$
- Sustituir diferentes valores de (x)
Para encontrar (A), (B), (C), (D), y (E), sustituimos diferentes valores de (x). Empezamos con (x = 0):
$$ 2 = A(0^2 + 1)^2 \Rightarrow A = 2 $$
- Uso de otros valores para simplificar calculaciones
Ahora, podemos usar otros valores como (x = 1) y (x = -1) para resolver el sistema de ecuaciones y encontrar los otros coeficientes.
Una vez que calculamos todos los coeficientes, obtenemos las fracciones parciales.
- Integración de cada término por separado
Una vez que tenemos la descomposición en fracciones parciales, integramos cada término:
$$ \int \frac{2}{x} dx + \int \frac{Bx+C}{x^2+1} dx + \int \frac{Dx + E}{(x^2 + 1)^2} dx $$
- Aplicar las fórmulas de integración
Usamos las siguientes fórmulas:
- $\int \frac{1}{x} dx = \ln |x| + C$
- $\int \frac{1}{x^2 + 1} dx = \tan^{-1}(x) + C$
- Para el último término, podemos usar una sustitución o una identidad de derivadas.
- Combinar todo
Finalmente, combinamos todos los resultados de las integrales y simplificamos.
La integral es
$$ 2 \ln |x| + B \tan^{-1}(x) + \frac{D}{2(x^2 + 1)} + C $$
More Information
Esta integral se usa con frecuencia en cálculo, especialmente en problemas que involucran funciones racionales. La descomposición en fracciones parciales es un método fundamental para resolver integrales más complejas.
Tips
- Olvidar multiplicar cada término correctamente al igualar numeradores.
- No simplificar adecuadamente las fracciones parciales después de integrarlas.
- Ignorar los términos de la constante de integración al final.
AI-generated content may contain errors. Please verify critical information