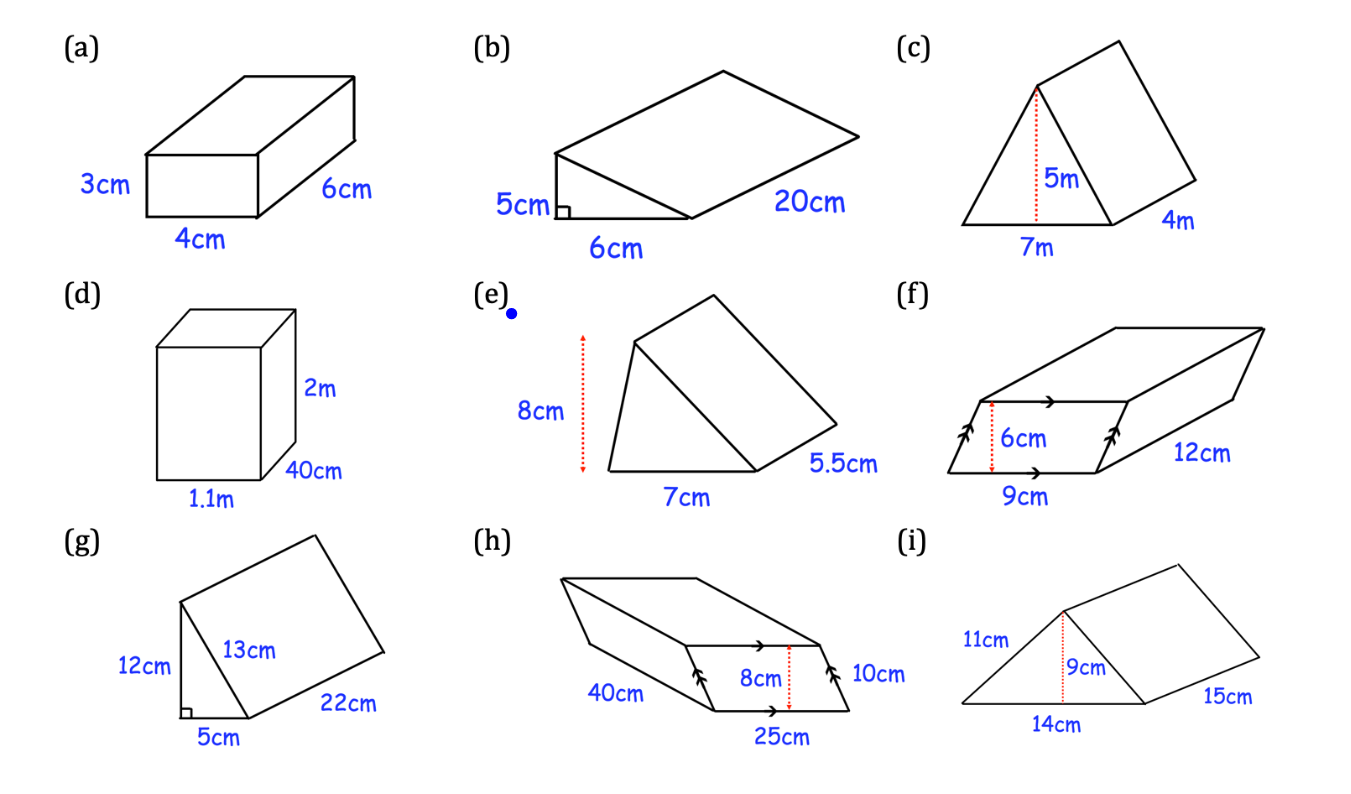
Calculate the volume of the shapes in the image.

Steps to Solve

Okay, let's break down how to find the volume of each of these shapes. We will use appropriate volume formulas for each shape.

1. (a) Rectangular Prism Volume

The volume $V$ of a rectangular prism is given by $V = l \times w \times h$, where $l$ is the length, $w$ is the width, and $h$ is the height. In this case, $l = 6$ cm, $w = 4$ cm, and $h = 3$ cm. So, $V = 6 \times 4 \times 3 = 72$ cubic centimeters.

2. (b) Triangular Prism Volume

The volume $V$ of a triangular prism is given by $V = A \times h$, where $A$ is the area of the triangular base, and $h$ is the height (or length) of the prism. The area of the triangle is $ A = \frac{1}{2} \times b \times h_t$, where $b$ is the base of the triangle, and $h_t$ is the height of the triangle. Here, $b = 6$ cm, $h_t = 5$ cm, and $h = 20$ cm. So, $A = \frac{1}{2} \times 6 \times 5 = 15$ square cm. Then, $V = 15 \times 20 = 300$ cubic centimeters.

3. (c) Triangular Prism Volume

Same as (b). Here, $b = 7$ m, $h_t = 5$ m, and $h = 4$ m. So, $A = \frac{1}{2} \times 7 \times 5 = 17.5$ square meters. Then, $V = 17.5 \times 4 = 70$ cubic meters.

4. (d) Rectangular Prism Volume

The volume $V$ of a rectangular prism is given by $V = l \times w \times h$. First, we need to convert all measurements to the same unit. Let's convert everything to meters. $l = 1.1$ m, $w = 40$ cm $= 0.4$ m, and $h = 2$ m. So, $V = 1.1 \times 0.4 \times 2 = 0.88$ cubic meters.

5. (e) Triangular Prism Volume

Same as (b). Here, $b = 7$ cm, $h_t = 8$ cm, and $h = 5.5$ cm. So, $A = \frac{1}{2} \times 7 \times 8 = 28$ square cm. Then, $V = 28 \times 5.5 = 154$ cubic centimeters.

6. (f) Parallelepiped Volume

The volume $V$ of a parallelepiped is given by $V = A \times h$, where $A$ is the area of the base, and $h$ is the height of the prism. The area of the parallelogram is $ A = b \times h_p$, where $b$ is the base of the parallelogram, and $h_p$ is the height of the parallelogram. Here, $b = 9$ cm, $h_p = 6$ cm, and $h = 12$ cm. So, $A = 9 \times 6 = 54$ square cm. Then, $V = 54 \times 12 = 648$ cubic centimeters.

7. (g) Triangular Prism Volume

Same as (b). Here, $b = 5$ cm, $h_t = 12$ cm, and $h = 22$ cm. So, $A = \frac{1}{2} \times 5 \times 12 = 30$ square cm. Then, $V = 30 \times 22 = 660$ cubic centimeters.

8. (h) Trapezoidal Prism Volume

The volume $V$ of a trapezoidal prism is given by $V = A \times h$, where $A$ is the area of the trapezoidal base, and $h$ is the height (or length) of the prism. The area of the trapezoid is $A = \frac{1}{2} \times (b_1 + b_2) \times h_t$ where $b_1$ and $b_2$ are the lengths of the parallel sides, and $h_t$ is the height of the trapezoid. Here, $b_1 = 25$ cm, $b_2 = 40$ cm, $h_t = 8$ cm, and $h = 10$ cm. So, $A = \frac{1}{2} \times (25 + 40) \times 8 = \frac{1}{2} \times 65 \times 8 = 260$ square cm. Then, $V = 260 \times 10 = 2600$ cubic centimeters.

9. (i) Triangular Prism Volume

Same as (b). Here, $b = 14$ cm, $h_t = 9$ cm, and $h = 15$ cm. So, $A = \frac{1}{2} \times 14 \times 9 = 63$ square cm. Then, $V = 63 \times 11 = 693$ cubic centimeters.