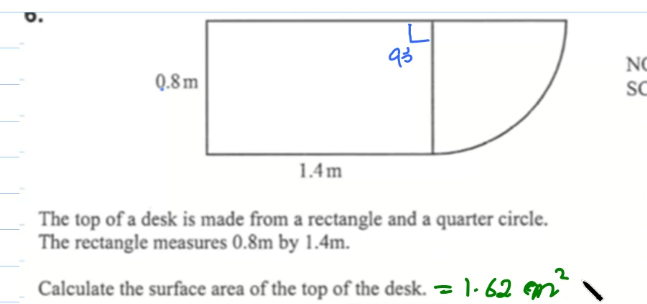
Calculate the surface area of the top of the desk.

Steps to Solve

1. Calculate the Area of the Rectangle

The area of the rectangle can be calculated using the formula:

$$ \text{Area}_{\text{rectangle}} = \text{length} \times \text{width} $$

Substituting the given dimensions:

$$ \text{Area}_{\text{rectangle}} = 1.4 , \text{m} \times 0.8 , \text{m} $$

2. Calculate the Area of the Quarter Circle

The area of a full circle is given by:

$$ \text{Area}_{\text{circle}} = \pi r^2 $$

Since we are dealing with a quarter circle, we will take a quarter of this area. The radius ( r ) corresponds to the width of the rectangle (0.8 m):

$$ \text{Area}_{\text{quarter circle}} = \frac{1}{4} \pi (0.8 , \text{m})^2 $$

3. Add Both Areas Together

Now, we combine the areas of the rectangle and the quarter circle to find the total surface area:

$$ \text{Total Surface Area} = \text{Area}{\text{rectangle}} + \text{Area}{\text{quarter circle}} $$

4. Substitute Values and Calculate

Now we put in the values we calculated:

First, compute the rectangle's area: $$ \text{Area}_{\text{rectangle}} = 1.4 \times 0.8 = 1.12 , \text{m}^2 $$

Next, compute the quarter circle's area: $$ \text{Area}_{\text{quarter circle}} = \frac{1}{4} \pi (0.8)^2 \approx \frac{1}{4} \pi (0.64) \approx 0.50265 , \text{m}^2 $$

Finally, add both areas: $$ \text{Total Surface Area} = 1.12 + 0.50265 \approx 1.62265 , \text{m}^2 $$