Calculate the slope of the graph of the following piecewise function at the points P(-1, 3) and P(2, 5): $f(x) = \begin{cases} 4 - x^2, & \text{if } x \leq 1 \\ 2x + 1, & \text{i... Calculate the slope of the graph of the following piecewise function at the points P(-1, 3) and P(2, 5): $f(x) = \begin{cases} 4 - x^2, & \text{if } x \leq 1 \\ 2x + 1, & \text{if } x > 1 \end{cases}$
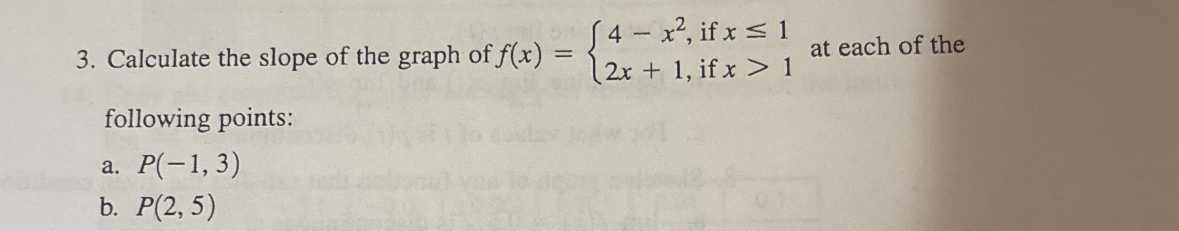
Understand the Problem
The question asks to calculate the slope of the graph of a piecewise function at two given points. We need to determine which piece of the function applies to each point and then find the derivative of that piece to evaluate the slope at the given x-value.
Answer
a. $2$ b. $2$
Answer for screen readers
a. The slope at $P(-1, 3)$ is $2$. b. The slope at $P(2, 5)$ is $2$.
Steps to Solve
- Determine which piece of the function to use for point P(-1, 3)
Since the x-coordinate of point P is -1, and $-1 \leq 1$, we use the first piece of the function: $f(x) = 4 - x^2$.
- Find the derivative of the first piece
To find the slope, we need to find the derivative of $f(x) = 4 - x^2$. $f'(x) = \frac{d}{dx}(4 - x^2) = -2x$
- Evaluate the derivative at x = -1
Substitute $x = -1$ into the derivative: $f'(-1) = -2(-1) = 2$
- Determine which piece of the function to use for point P(2, 5)
Since the x-coordinate of point P is 2, and $2 > 1$, we use the second piece of the function: $f(x) = 2x + 1$.
- Find the derivative of the second piece
To find the slope, we need to find the derivative of $f(x) = 2x + 1$. $f'(x) = \frac{d}{dx}(2x + 1) = 2$
- Evaluate the derivative at x = 2
The derivative of $2x + 1$ is a constant, so $f'(2) = 2$.
a. The slope at $P(-1, 3)$ is $2$. b. The slope at $P(2, 5)$ is $2$.
More Information
The derivative of a function at a point gives the slope of the tangent line to the function at that point. In this case, we found the derivatives of the respective pieces of the piecewise function and evaluated them at the given points.
Tips
A common mistake is to use the wrong piece of the function for a given point. It is crucial to check the condition ($x \leq 1$ or $x > 1$) to determine which piece applies. Another common mistake is incorrectly calculating the derivative. Remember the power rule and constant rule for differentiation.
AI-generated content may contain errors. Please verify critical information