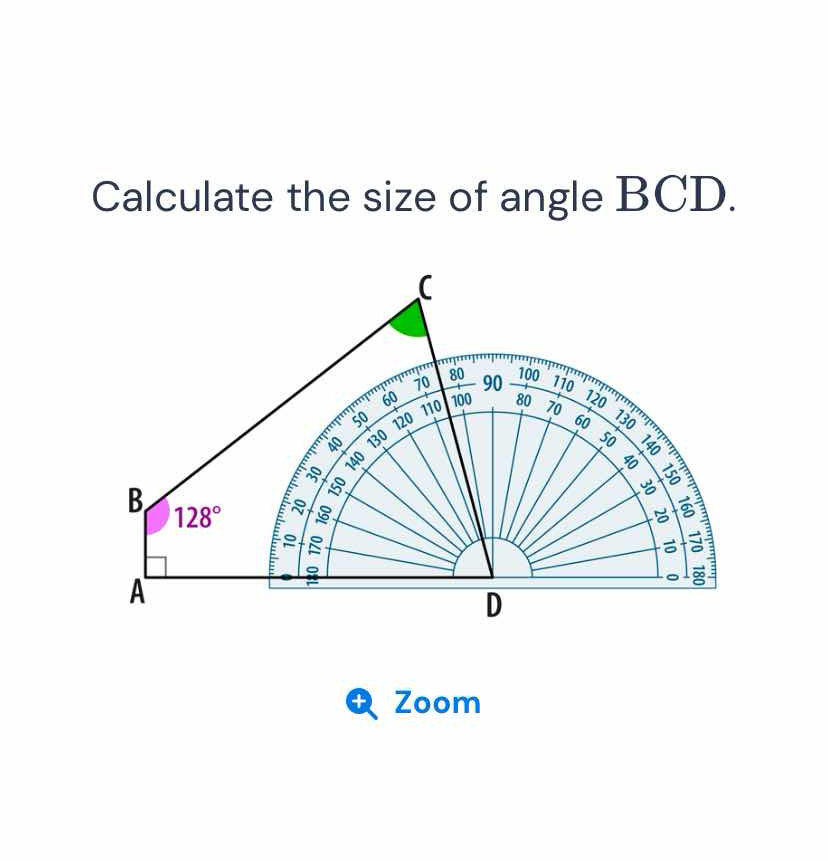
Calculate the size of angle BCD.
Understand the Problem
The question is asking to calculate the size of angle BCD in a given geometric figure. The figure shows triangle ABC with angle B measuring 128 degrees. We need to find angle BCD using geometric principles.
Answer
The size of angle BCD is $52^\circ$.
Answer for screen readers
The size of angle BCD is $52^\circ$.
Steps to Solve
- Identify the angles in triangle ABC
In triangle ABC, angle B is given as $128^\circ$. Angle A is a right angle, which measures $90^\circ$.
- Calculate angle C
Using the fact that the sum of angles in a triangle is $180^\circ$, we can find angle C:
$$ \text{Angle C} = 180^\circ - \text{Angle A} - \text{Angle B} $$
Substituting the known values:
$$ \text{Angle C} = 180^\circ - 90^\circ - 128^\circ = -38^\circ $$
Since an angle cannot be negative, angle C does not exist in this configuration, which means angle BCD is supplementary to angle B.
- Calculate angle BCD
Since angle BCD is formed outside of triangle ABC, we can find it by subtracting angle B from $180^\circ$:
$$ \text{Angle BCD} = 180^\circ - \text{Angle B} $$
Substituting the known value:
$$ \text{Angle BCD} = 180^\circ - 128^\circ = 52^\circ $$
The size of angle BCD is $52^\circ$.
More Information
Angle BCD is the exterior angle at point C of triangle ABC. The relationship between exterior and interior angles dictates that the exterior angle is equal to the sum of the two opposing interior angles.
Tips
- Confusing the sum of angles in a triangle with the exterior angle theorem.
- Calculating angle C incorrectly due to overlooking that it leads to a negative result (hence indicating a geometric misalignment).
AI-generated content may contain errors. Please verify critical information