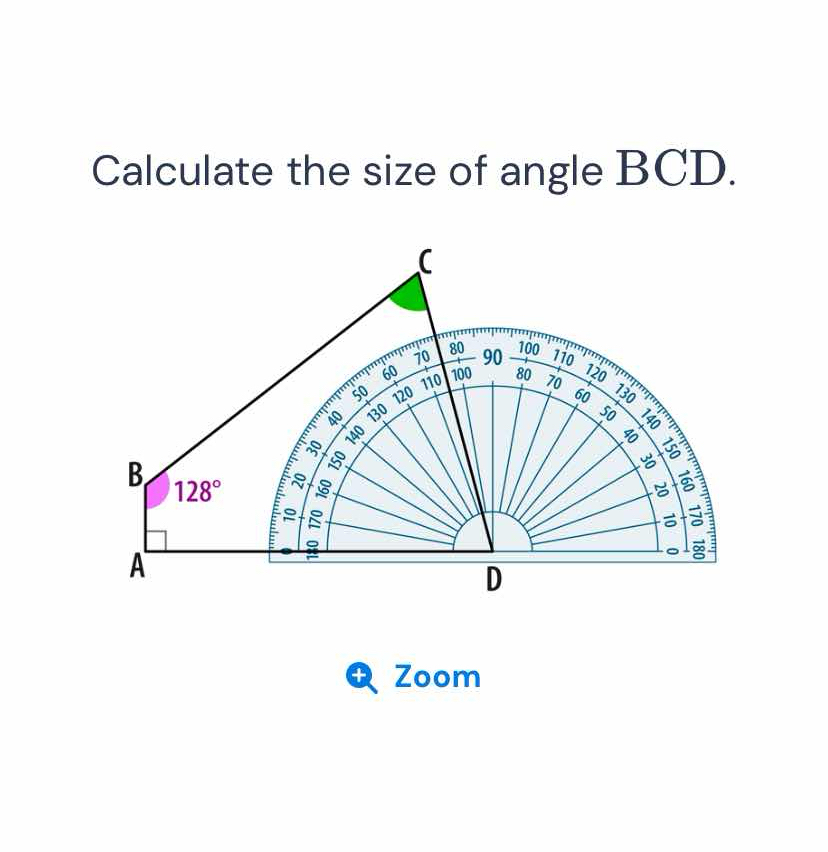
Calculate the size of angle BCD.
Understand the Problem
The question is asking to calculate the size of angle BCD given that angle ABC is 128 degrees. To find the value of angle BCD, one can utilize the property that the sum of angles in a straight line is equal to 180 degrees.
Answer
The size of angle BCD is $52^\circ$.
Answer for screen readers
The size of angle BCD is $52^\circ$.
Steps to Solve
-
Identify the known angle
The known angle is $ \angle ABC = 128^\circ $. -
Use the straight angle property
The angles on a straight line sum up to $180^\circ$. Since angles $ \angle ABC $ and $ \angle BCD $ are on the same straight line BD, we can write:
$$ \angle ABC + \angle BCD = 180^\circ $$ -
Substitute the known angle into the equation
Substituting $128^\circ$ into the equation gives:
$$ 128^\circ + \angle BCD = 180^\circ $$ -
Solve for $ \angle BCD $
Rearranging gives:
$$ \angle BCD = 180^\circ - 128^\circ $$
Calculating the above will result in:
$$ \angle BCD = 52^\circ $$
The size of angle BCD is $52^\circ$.
More Information
Angle BCD is complementary with angle ABC since they are on a straight line. This relationship is a fundamental aspect of geometry that helps calculate unknown angles easily.
Tips
null
AI-generated content may contain errors. Please verify critical information