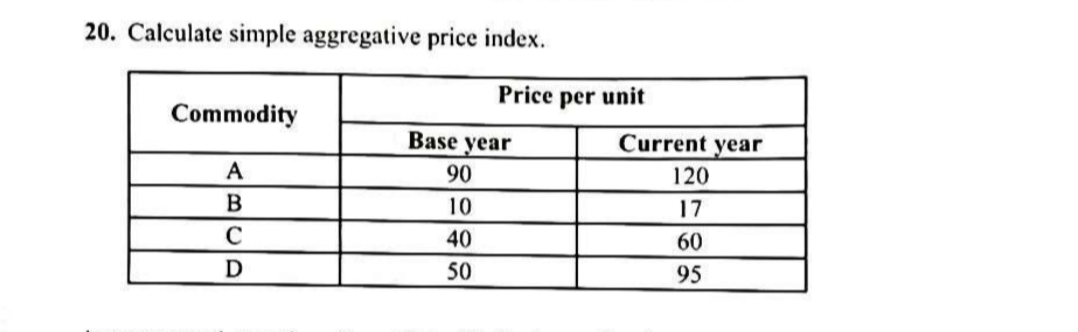
Calculate the simple aggregative price index.
Understand the Problem
The question asks to calculate the simple aggregate price index given the price per unit for different commodities in the base year and the current year. To solve this, you will first sum the prices in the base year, sum the prices in the current year, and then apply the formula for the simple aggregate price index.
Answer
$153.68$
Answer for screen readers
The simple aggregate price index is $153.68$.
Steps to Solve
- Calculate the sum of prices in the base year
Add the prices of all commodities in the base year: $90 + 10 + 40 + 50 = 190$
- Calculate the sum of prices in the current year
Add the prices of all commodities in the current year: $120 + 17 + 60 + 95 = 292$
- Apply the Simple Aggregate Price Index Formula
The formula for the simple aggregate price index is: $$ \text{Simple Aggregate Price Index} = \frac{\sum \text{Current year prices}}{\sum \text{Base year prices}} \times 100 $$ Substitute the calculated sums into the formula: $$ \text{Simple Aggregate Price Index} = \frac{292}{190} \times 100 $$
- Calculate the Index
Divide 292 by 190, and then multiply by 100: $$ \frac{292}{190} \times 100 = 1.5368421 \times 100 = 153.68421 $$ Round to two decimal places: 153.68
The simple aggregate price index is $153.68$.
More Information
The Simple Aggregate Price Index measures the change in the overall price level of a group of items (commodities) from a base period to a current period. An index value of $153.68$ suggests there has been a $53.68%$ increase in the price level compared to the base year.
Tips
A common mistake is to forget to multiply the ratio of the sums by 100, which is necessary to express the index as a percentage. Another mistake is incorrect summation of the prices.
AI-generated content may contain errors. Please verify critical information