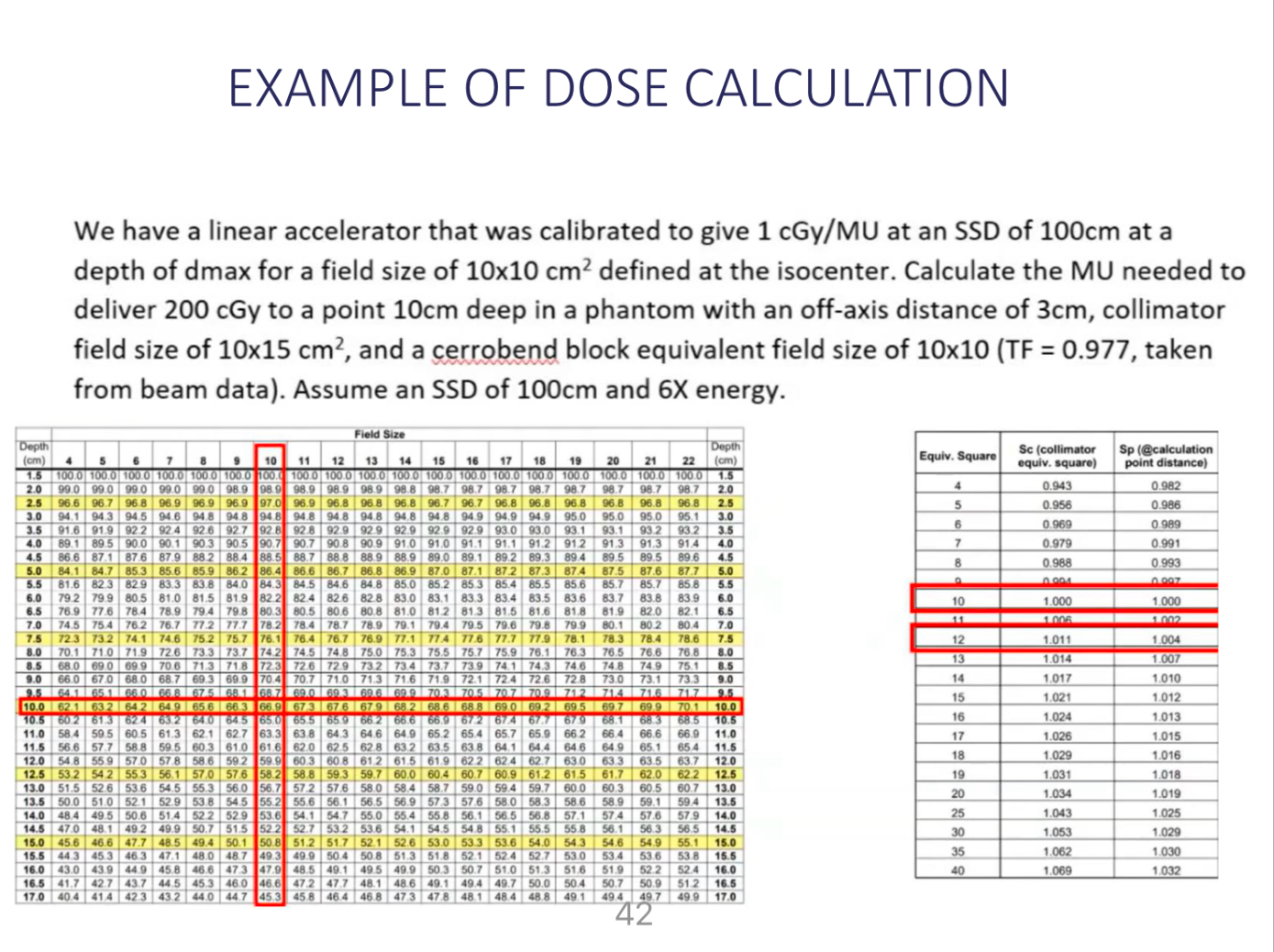
Calculate the MU needed to deliver 200 cGy to a point 10 cm deep in a phantom with an off-axis distance of 3 cm, given the parameters from the linear accelerator calibration.

Steps to Solve

1. Identify Key Values Given the scenario, we need to gather the key values:

• Desired dose: 200 cGy
• Depth: 10 cm
• Off-axis distance: 3 cm
• Collimator field size: 10 cm x 15 cm
• Equivalent field size: 10 cm x 10 cm
• Sc (collimator equivalent square) factor and dose factors as per the table.

2. Determine the Dose from MU Calculation From the calibration, we know: $$ \text{Dose delivered} = \text{MU} \times \text{Calibration factor} $$

Given that the calibration factor is 1 cGy/MU, we can express the dose in terms of MU: $$ 200 \text{ cGy} = \text{MU} \times 1 \text{ cGy/MU} $$

This allows us to simplify the equation: $$ \text{MU} = 200 $$

3. Apply Correction Factors Next, we must apply the correction factors from the provided tables to account for:

• Depth dose (DD) at 10 cm.
• Collimator equivalent square correction factor (Sc).
• Tissue phantom ratio (TF).

From the dose calculation table for depth = 10 cm and field size 10x10 cm, we find: Depth dose (at 10 cm) = 67.4% (from the table).

Using the Sc factor from the right table at 10 cm:

• Sc = 1.000

4. Calculate Final MU Now we adjust for depth and field size: $$ \text{MU} = \frac{200 \text{ cGy}}{0.674 \times 1.000} $$

Calculating: $$ \text{MU} = \frac{200}{0.674} \approx 296.3 $$

5. Rounding Typically, you would round the MU to the nearest whole number for practical application: $$ \text{MU} \approx 296 $$