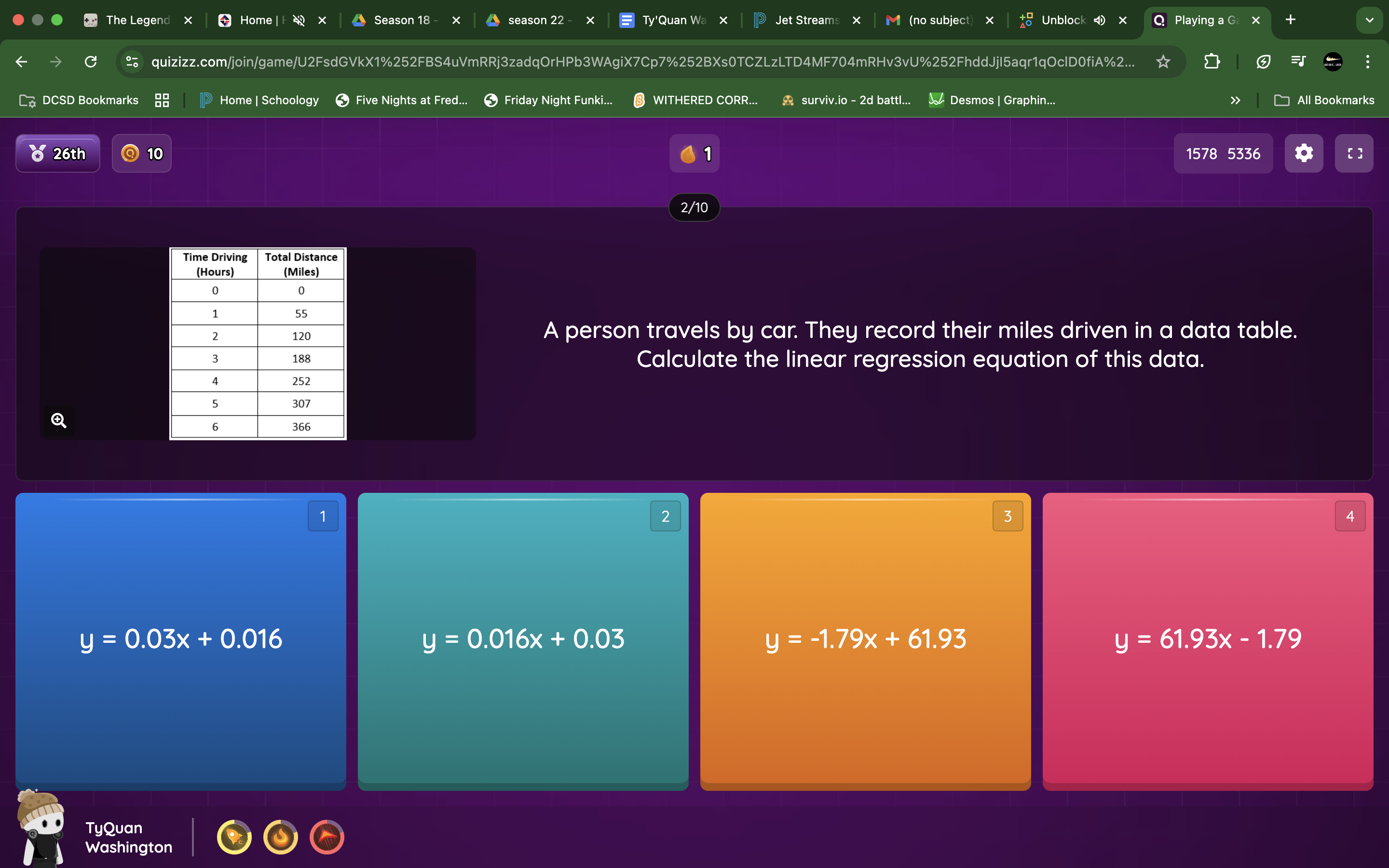
Calculate the linear regression equation of the given data table.

Steps to Solve

1. Calculate the means of x and y

First, find the average of the x values (time driving) and the y values (total distance). $$ \bar{x} = \frac{0 + 1 + 2 + 3 + 4 + 5 + 6}{7} = \frac{21}{7} = 3 $$ $$ \bar{y} = \frac{0 + 55 + 120 + 188 + 252 + 307 + 366}{7} = \frac{1288}{7} = 184 $$

2. Calculate the slope (m) of the regression line

The formula for the slope $m$ is: $$ m = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2} $$ Calculate the terms: $$ \sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y}) = (0-3)(0-184) + (1-3)(55-184) + (2-3)(120-184) + (3-3)(188-184) + (4-3)(252-184) + (5-3)(307-184) + (6-3)(366-184) $$ $$ = (-3)(-184) + (-2)(-129) + (-1)(-64) + (0)(4) + (1)(68) + (2)(123) + (3)(182) $$ $$ = 552 + 258 + 64 + 0 + 68 + 246 + 546 = 1734$$

Calculate the denominator: $$ \sum_{i=1}^{n}(x_i - \bar{x})^2 = (0-3)^2 + (1-3)^2 + (2-3)^2 + (3-3)^2 + (4-3)^2 + (5-3)^2 + (6-3)^2 $$ $$ = (-3)^2 + (-2)^2 + (-1)^2 + (0)^2 + (1)^2 + (2)^2 + (3)^2 $$ $$ = 9 + 4 + 1 + 0 + 1 + 4 + 9 = 28 $$

So, the slope $m$ is: $$ m = \frac{1734}{28} = 61.92857 \approx 61.93$$

3. Calculate the y-intercept (b) of the regression line

The formula for the y-intercept $b$ is: $$ b = \bar{y} - m\bar{x} $$ $$ b = 184 - (61.93)(3) = 184 - 185.79 = -1.79$$

4. Write the linear regression equation

The linear regression equation is in the form $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. $$ y = 61.93x - 1.79 $$