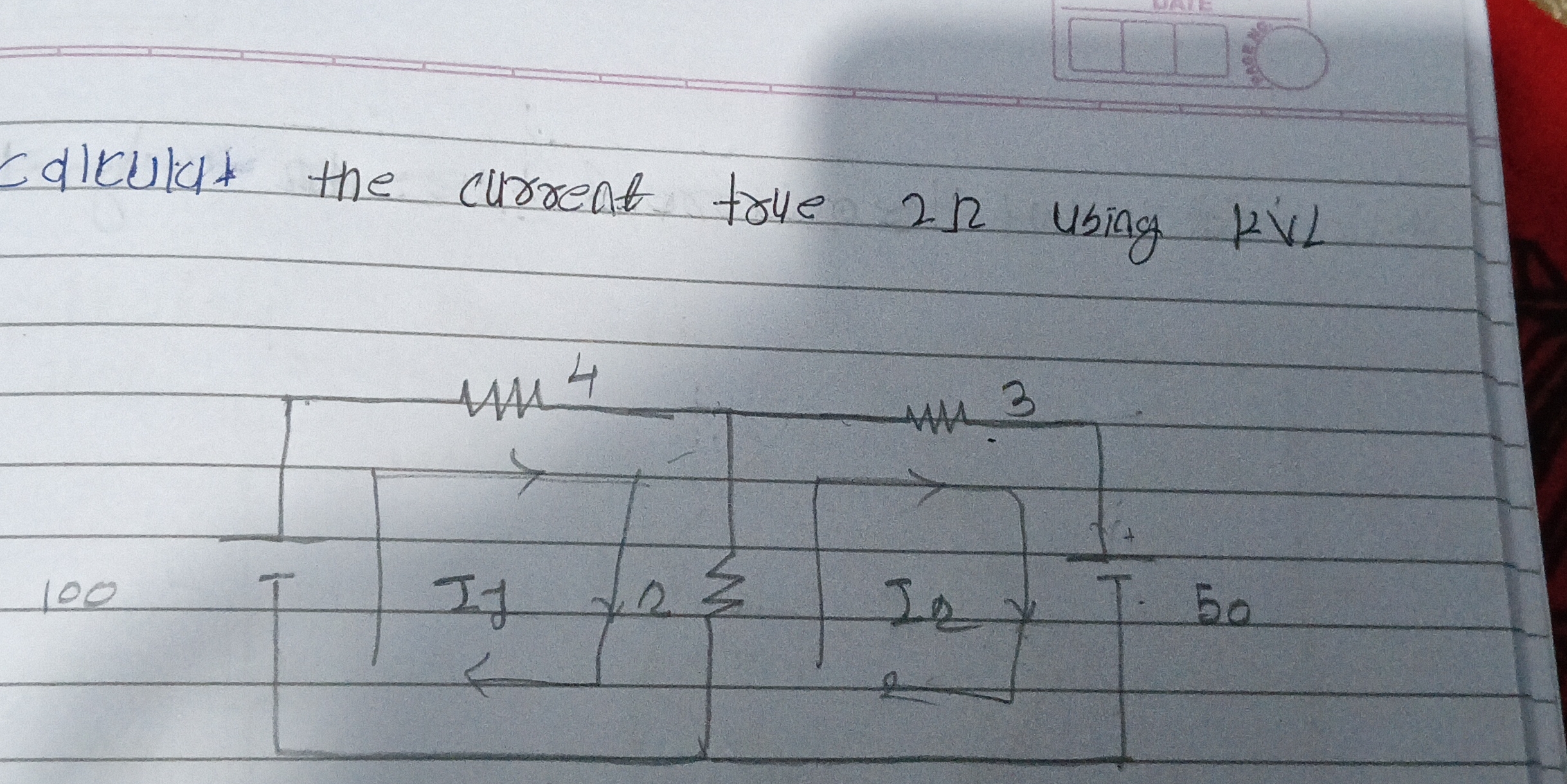
Calculate the current through the 2 Ohm resistor using KVL.
Understand the Problem
The question is asking to calculate the current through the 2 Ohm resistor in the circuit using Kirchhoff's Voltage Law (KVL). KVL states that the sum of all voltage drops in a closed loop is equal to zero. We will need to apply KVL to each loop in the circuit to setup our equations, and then solve for the currents.
Answer
$\frac{50}{13} \text{ A}$
Answer for screen readers
The current through the 2$\Omega$ resistor is $\frac{50}{13} \text{ A} \approx 3.85 \text{ A}$.
Steps to Solve
- Apply KVL to Loop 1.
Starting from the 100V source and moving clockwise, the voltage drops are:
$$-100 + 4I_1 + 2(I_1 - I_2) = 0$$
Simplifying the equation:
$$6I_1 - 2I_2 = 100$$
Dividing by 2:
$$3I_1 - I_2 = 50 \hspace{1cm} (1)$$
- Apply KVL to Loop 2.
Starting from the 50V source and moving clockwise, the voltage drops are:
$$-50 + 3I_2 + 2(I_2 - I_1) = 0$$
Simplifying the equation:
$$-2I_1 + 5I_2 = 50 \hspace{1cm} (2)$$
- Solve the system of equations.
We now have two equations:
$$3I_1 - I_2 = 50 \hspace{1cm} (1)$$
$$-2I_1 + 5I_2 = 50 \hspace{1cm} (2)$$
Multiplying equation (1) by 5 gives:
$$15I_1 - 5I_2 = 250 \hspace{1cm} (3)$$
Adding equation (2) and (3) to eliminate $I_2$
$$13I_1 = 300$$
$$I_1 = \frac{300}{13} \approx 23.08 \text{ A}$$
- Solve for $I_2$.
Substitute $I_1$ back into equation (1):
$$3(\frac{300}{13}) - I_2 = 50$$
$$I_2 = \frac{900}{13} - 50 = \frac{900 - 650}{13} = \frac{250}{13} \approx 19.23 \text{ A}$$
- Calculate the current through the 2$\Omega$ resistor.
The current through the 2$\Omega$ resistor is $I_1 - I_2$. Thus,
$$I_{2\Omega} = I_1 - I_2 = \frac{300}{13} - \frac{250}{13} = \frac{50}{13} \approx 3.85 \text{ A}$$
The current through the 2$\Omega$ resistor is $\frac{50}{13} \text{ A} \approx 3.85 \text{ A}$.
More Information
The positive value indicates the net current flows in the assumed direction (from left to right in the original diagram).
Tips
A common mistake would be to make an error when setting up the KVL equations (e.g., incorrect signs for voltage drops/rises or not accounting for the current source). Another common mistake is making algebraic errors when solving the system of equations.
AI-generated content may contain errors. Please verify critical information