Calculate the arithmetic mean of the following series. Use the short-cut method and take 15 as the assumed average: Size: 20, 19, 18, 17, 16, 15, 14, 13, 12, 11 Frequency: 1, 2, 4... Calculate the arithmetic mean of the following series. Use the short-cut method and take 15 as the assumed average: Size: 20, 19, 18, 17, 16, 15, 14, 13, 12, 11 Frequency: 1, 2, 4, 8, 11, 10, 7, 4, 2, 1
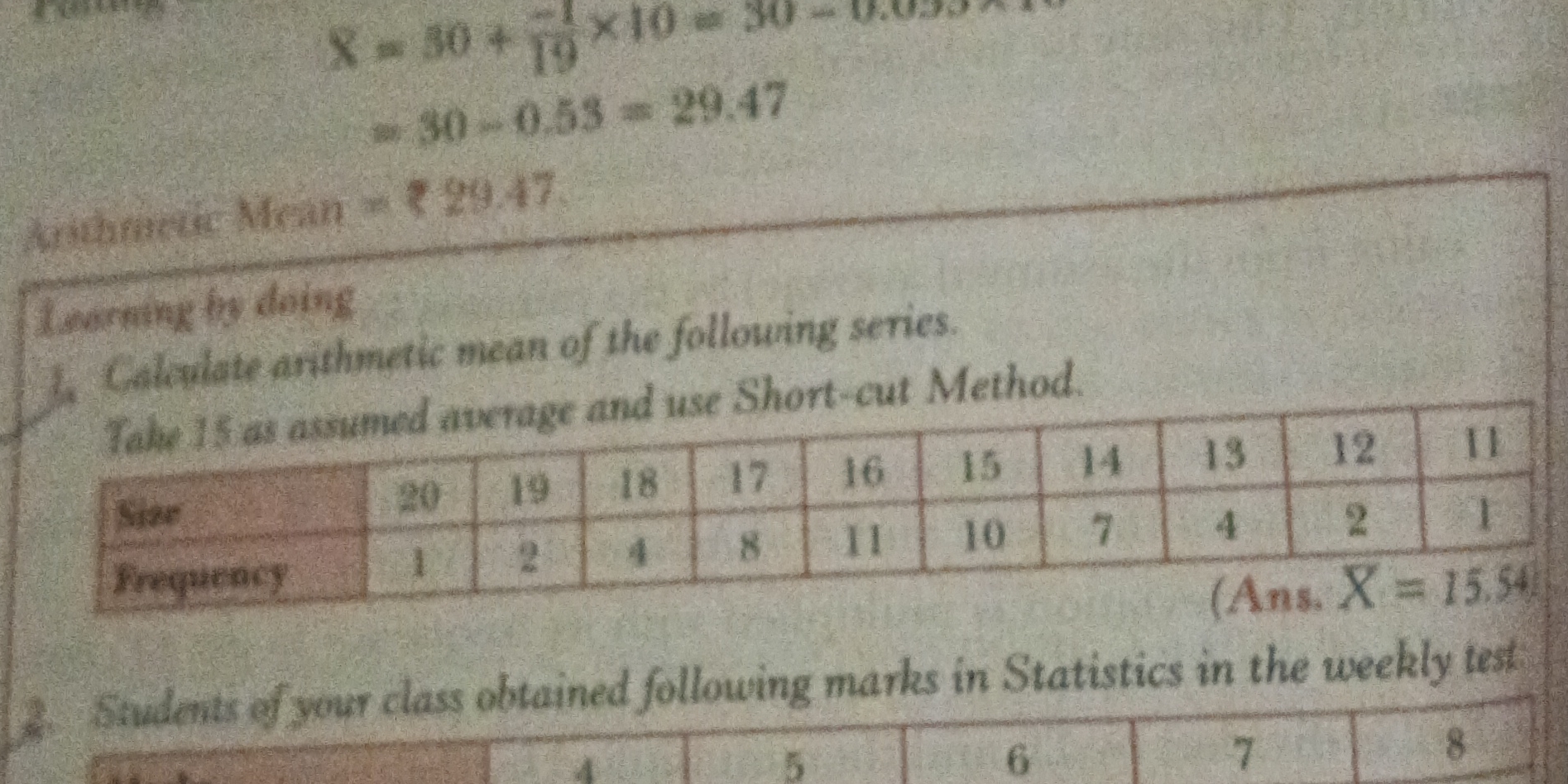
Understand the Problem
The question asks to calculate the arithmetic mean of a given series using the short-cut method, assuming 15 as the average. We are given the size and frequency of each item in the series and need to calculate the mean. To accomplish this, we'll determine the deviation from the assumed mean for each size, multiply by the frequency, sum these products, and then use the short-cut formula to calculate the arithmetic mean.
Answer
$Arithmetic Mean = 15.54$
Answer for screen readers
$Arithmetic Mean = 15.54$
Steps to Solve
- Calculate the deviation ($d_i$) from the assumed mean for each size
The assumed mean is 15. We subtract this from each size ($x_i$) to get the deviation $d_i = x_i - 15$.
$d_1 = 20 - 15 = 5$ $d_2 = 19 - 15 = 4$ $d_3 = 18 - 15 = 3$ $d_4 = 17 - 15 = 2$ $d_5 = 16 - 15 = 1$ $d_6 = 15 - 15 = 0$ $d_7 = 14 - 15 = -1$ $d_8 = 13 - 15 = -2$ $d_9 = 12 - 15 = -3$ $d_{10} = 11 - 15 = -4$
- Multiply each deviation ($d_i$) by its corresponding frequency ($f_i$)
We multiply the deviations calculated in the previous step by their corresponding frequencies to find $f_i d_i$.
$f_1 d_1 = 1 \times 5 = 5$ $f_2 d_2 = 2 \times 4 = 8$ $f_3 d_3 = 4 \times 3 = 12$ $f_4 d_4 = 8 \times 2 = 16$ $f_5 d_5 = 11 \times 1 = 11$ $f_6 d_6 = 10 \times 0 = 0$ $f_7 d_7 = 7 \times -1 = -7$ $f_8 d_8 = 4 \times -2 = -8$ $f_9 d_9 = 2 \times -3 = -6$ $f_{10} d_{10} = 1 \times -4 = -4$
- Calculate the sum of the products of frequency and deviation ($\sum f_i d_i$)
We add all the $f_i d_i$ values calculated in the previous step.
$\sum f_i d_i = 5 + 8 + 12 + 16 + 11 + 0 - 7 - 8 - 6 - 4 = 27$
- Calculate the sum of the frequencies ($\sum f_i$)
We add all the frequencies.
$\sum f_i = 1 + 2 + 4 + 8 + 11 + 10 + 7 + 4 + 2 + 1 = 50$
- Apply the short-cut method formula
The short-cut method formula for calculating the arithmetic mean is: $Arithmetic Mean = A + \frac{\sum f_i d_i}{\sum f_i}$, where A is the assumed mean.
$Arithmetic Mean = 15 + \frac{27}{50}$
$Arithmetic Mean = 15 + 0.54$
$Arithmetic Mean = 15.54$
$Arithmetic Mean = 15.54$
More Information
The short-cut method simplifies the calculation of the mean by using an assumed mean and focusing on deviations, especially useful when dealing with larger numbers.
Tips
A common mistake is making errors in calculating the deviations ($d_i$) or in multiplying the deviations by the frequencies ($f_i d_i$). Another common mistake is in the arithmetic when summing the $f_i d_i$ values or the frequencies ($f_i$). Ensuring careful calculation at each step can prevent these errors.
AI-generated content may contain errors. Please verify critical information