Calculate the area of the given shape.
Understand the Problem
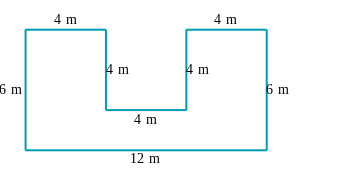
The question involves calculating the area of a composite shape formed by rectangles. The dimensions provided indicate the lengths of various sides, and the goal is to determine the total area.
Answer
The total area is \( 56 \, m^2 \).
Answer for screen readers
The total area of the composite shape is ( 56 , m^2 ).
Steps to Solve
- Identify the Shape Components
The composite shape can be divided into three distinct rectangles: the large rectangle, the smaller rectangle in the middle, and the two side rectangles.
- Calculating the Area of the Large Rectangle
The dimensions of the large rectangle are 12 m (length) and 6 m (height). The area is calculated as: $$ \text{Area}_{large} = \text{length} \times \text{height} = 12 , m \times 6 , m = 72 , m^2 $$
- Calculating the Area of the Middle Rectangle
The dimensions of the middle rectangle are 4 m (length) and 4 m (height). The area is calculated as: $$ \text{Area}_{middle} = \text{length} \times \text{height} = 4 , m \times 4 , m = 16 , m^2 $$
- Calculating the Total Area
Now, add the area of the large rectangle and the area of the middle rectangle to find the total area of the composite shape: $$ \text{Total Area} = \text{Area}{large} + \text{Area}{middle} $$
- Final Calculation of Total Area
Substituting the previously calculated areas: $$ \text{Total Area} = 72 , m^2 - 16 , m^2 = 56 , m^2 $$
The total area of the composite shape is ( 56 , m^2 ).
More Information
The shape consists of two rectangles with the same height and a larger rectangle, giving us a straightforward way to calculate the total area by addition and subtraction of the included areas.
Tips
- Forgetting to account for overlapping areas when calculating the total area.
- Miscalculating any of the rectangle dimensions.
AI-generated content may contain errors. Please verify critical information