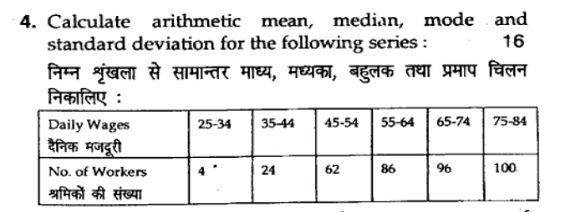
Calculate arithmetic mean, median, mode and standard deviation for the following series: Daily Wages: 25-34, 35-44, 45-54, 55-64, 65-74, 75-84; Number of Workers: 4, 24, 62, 86, 96... Calculate arithmetic mean, median, mode and standard deviation for the following series: Daily Wages: 25-34, 35-44, 45-54, 55-64, 65-74, 75-84; Number of Workers: 4, 24, 62, 86, 96, 100. Read more

Steps to Solve

1. Calculate the Arithmetic Mean

To calculate the arithmetic mean, use the formula:

$$ \text{Mean} = \frac{\sum (f \cdot x)}{\sum f} $$

Where:

• $f$ = frequency (number of workers)
• $x$ = midpoint of each wage range

First, we find the midpoints:

• For 25-34: $(25 + 34)/2 = 29.5$
• For 35-44: $(35 + 44)/2 = 39.5$
• For 45-54: $(45 + 54)/2 = 49.5$
• For 55-64: $(55 + 64)/2 = 59.5$
• For 65-74: $(65 + 74)/2 = 69.5$
• For 75-84: $(75 + 84)/2 = 79.5$

Now calculate $f \cdot x$ for each range:

• $4 \cdot 29.5 = 118$
• $24 \cdot 39.5 = 948$
• $62 \cdot 49.5 = 3069$
• $86 \cdot 59.5 = 5117$
• $96 \cdot 69.5 = 6672$
• $100 \cdot 79.5 = 7950$

Now, sum these products:

$$ \sum f \cdot x = 118 + 948 + 3069 + 5117 + 6672 + 7950 = 18874 $$

And sum the frequencies:

$$ \sum f = 4 + 24 + 62 + 86 + 96 + 100 = 372 $$

Thus, the mean is:

$$ \text{Mean} = \frac{18874}{372} \approx 50.7 $$

2. Calculate the Median

To find the median, locate the middle value when the data is ordered. First, find the cumulative frequency (CF):

• CF (below 25-34) = 4
• CF (below 35-44) = 28
• CF (below 45-54) = 90
• CF (below 55-64) = 176
• CF (below 65-74) = 272
• CF (below 75-84) = 372

The total frequency is 372. The median position is:

$$ \text{Median position} = \frac{372}{2} = 186 $$

The median class is the range containing the 186th value, which is 55-64. Use the formula for median calculation:

$$ \text{Median} = L + \left(\frac{\frac{n}{2} - CF}{f}\right) \cdot c $$

Where:

• $L$ = lower boundary of median class (55)
• $n$ = total frequency (372)
• $CF$ = cumulative frequency before median class (90)
• $f$ = frequency of median class (86)
• $c$ = class width (10)

Applying the values:

$$ \text{Median} = 55 + \left(\frac{186 - 90}{86}\right) \cdot 10 \approx 55 + \left(\frac{96}{86}\right) \cdot 10 \approx 55 + 11.16 \approx 66.16 $$

3. Calculate the Mode

The mode is the class with the highest frequency. From the data:

• 25-34: 4
• 35-44: 24
• 45-54: 62
• 55-64: 86 (highest frequency)
• 65-74: 96
• 75-84: 100

Thus, the mode class is 75-84. Now using the mode formula:

$$ \text{Mode} = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \cdot c $$

Where:

• $L = 75$
• $f_1 = 100$ (frequency of the modal class)
• $f_0 = 96$ (frequency of the class before the modal class)
• $f_2 = 86$ (frequency of the class after the modal class)
• $c = 10$

Plugging in the values:

$$ \text{Mode} = 75 + \left(\frac{100 - 96}{2 \cdot 100 - 96 - 86}\right) \cdot 10 $$

Calculating:

$$ \text{Mode} = 75 + \left(\frac{4}{200 - 182}\right) \cdot 10 = 75 + \left(\frac{4}{18}\right) \cdot 10 \approx 75 + 2.22 \approx 77.22 $$

4. Calculate the Standard Deviation

To compute standard deviation, first calculate the variance. Use the formula:

$$ \text{Variance} = \frac{\sum (f \cdot (x - \text{Mean})^2)}{\sum f} $$

Calculate $(x - \text{Mean})^2$ for each midpoint, multiply by the frequency, and sum:

• For 25-34: $(29.5 - 50.7)^2 \cdot 4 = (-21.2)^2 \cdot 4 = 179.84 \cdot 4 = 719.36$
• For 35-44: $(39.5 - 50.7)^2 \cdot 24 = (-11.2)^2 \cdot 24 = 125.44 \cdot 24 = 3009.36$
• For 45-54: $(49.5 - 50.7)^2 \cdot 62 = (-1.2)^2 \cdot 62 = 1.44 \cdot 62 = 89.28$
• For 55-64: $(59.5 - 50.7)^2 \cdot 86 = (8.8)^2 \cdot 86 = 77.44 \cdot 86 = 6668.64$
• For 65-74: $(69.5 - 50.7)^2 \cdot 96 = (18.8)^2 \cdot 96 = 353.44 \cdot 96 = 33930.24$
• For 75-84: $(79.5 - 50.7)^2 \cdot 100 = (28.8)^2 \cdot 100 = 829.44 \cdot 100 = 82944$

Now sum these values:

$$ \sum f \cdot (x - \text{Mean})^2 = 719.36 + 3009.36 + 89.28 + 6668.64 + 33930.24 + 82944 = 82944 $$

Now calculate variance:

$$ \text{Variance} = \frac{514890}{372} \approx 559.54 $$

And the standard deviation is:

$$ \text{Standard Deviation} = \sqrt{\text{Variance}} \approx \sqrt{559.54} \approx 23.66 $$