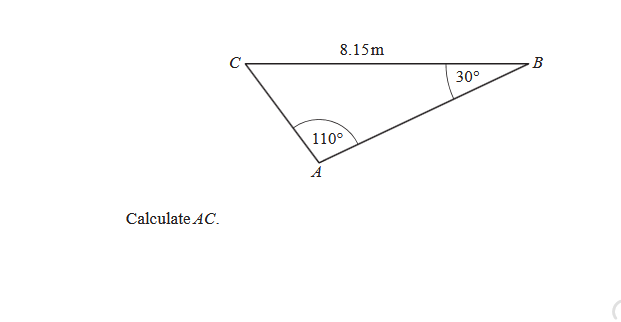
Calculate AC.

Steps to Solve

1. Identify Known Values We have triangle ABC with:

• Side ( CB = 8.15 , \text{m} )
• Angle ( A = 110^\circ )
• Angle ( B = 30^\circ )

2. Calculate Angle C We can find the third angle ( C ) using the fact that the sum of angles in a triangle equals ( 180^\circ ): $$ C = 180^\circ - A - B $$ $$ C = 180^\circ - 110^\circ - 30^\circ = 40^\circ $$

3. Apply the Sine Rule Using the Sine Rule which states: $$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$

We will use it to find ( AC ):

• Let ( AC = b )
• Then, based on supported angles: $$ \frac{b}{\sin B} = \frac{CB}{\sin C} $$

4. Substitute Known Values in Sine Rule Substituting the values into the Sine Rule: $$ \frac{AC}{\sin 30^\circ} = \frac{8.15 , \text{m}}{\sin 40^\circ} $$

5. Solve for AC Now, we can solve for ( AC ): $$ AC = \frac{8.15 , \text{m} \cdot \sin 30^\circ}{\sin 40^\circ} $$

6. Calculate the Values First, we know:

• ( \sin 30^\circ = 0.5 )
• ( \sin 40^\circ \approx 0.6428 )

Now performing the calculation: $$ AC = \frac{8.15 \cdot 0.5}{0.6428} $$

7. Final Calculation Calculate the length of ( AC ): $$ AC \approx \frac{4.075}{0.6428} \approx 6.35 , \text{m} $$