Berechne die Inverse von A.
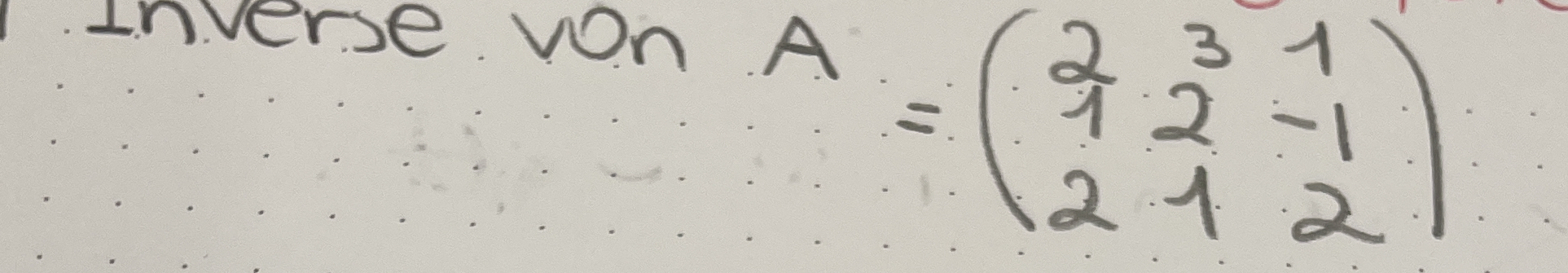
Understand the Problem
Die Frage fragt nach der Berechnung der Inversen einer Matrix A, die im Bild angegeben ist.
Answer
$$ A^{-1} = \begin{pmatrix} -\frac{3}{14} & \frac{3}{7} & 0 \\ \frac{5}{14} & -\frac{1}{7} & -\frac{2}{7} \\ \frac{2}{7} & 0 & \frac{2}{7} \end{pmatrix} $$
Answer for screen readers
$$ A^{-1} = \begin{pmatrix} -\frac{3}{14} & \frac{3}{7} & 0 \ \frac{5}{14} & -\frac{1}{7} & -\frac{2}{7} \ \frac{2}{7} & 0 & \frac{2}{7} \end{pmatrix} $$
Steps to Solve
- Matrix aufsetzen
Die Matrix $A$ ist gegeben durch: $$ A = \begin{pmatrix} 2 & 3 & 1 \ 2 & 1 & -1 \ 2 & 1 & 2 \end{pmatrix} $$
- Determinante berechnen
Um die Inverse zu finden, müssen wir zuerst die Determinante von $A$ berechnen. Die Determinante für eine $3 \times 3$ Matrix wird folgendermaßen berechnet: $$ \text{det}(A) = a(ei-fh) - b(di-fg) + c(dh-eg) $$ Für die Matrix $A$ haben wir:
$$ \text{det}(A) = 2 \cdot (1\cdot2 - (-1)\cdot1) - 3 \cdot (2\cdot2 - (-1)\cdot2) + 1 \cdot (2\cdot1 - 2\cdot2) $$
Das ergibt: $$ \text{det}(A) = 2 \cdot (2 + 1) - 3 \cdot (4 + 2) + 1 \cdot (2 - 4) $$ $$ = 2 \cdot 3 - 3 \cdot 6 - 2 = 6 - 18 - 2 = -14 $$
- Adjungierte Matrix berechnen
Nun berechnen wir die adjungierte Matrix $A^*$, die aus den Minoren und Cofaktoren besteht. Wir bestimmen die Cofaktoren:
- $C_{11} = \text{det} \begin{pmatrix} 1 & -1 \ 1 & 2 \end{pmatrix} = 1\cdot2 - (-1)\cdot1 = 3$
- $C_{12} = -\text{det} \begin{pmatrix} 2 & -1 \ 2 & 2 \end{pmatrix} = -(2\cdot2 - (-1)\cdot2) = -6$
- $C_{13} = \text{det} \begin{pmatrix} 2 & 1 \ 2 & 1 \end{pmatrix} = 2\cdot1 - 1\cdot2 = 0$
- $C_{21} = -\text{det} \begin{pmatrix} 3 & 1 \ 1 & 2 \end{pmatrix} = -(3\cdot2 - 1\cdot1) = -5$
- $C_{22} = \text{det} \begin{pmatrix} 2 & 1 \ 2 & 2 \end{pmatrix} = 2\cdot2 - 1\cdot2 = 2$
- $C_{23} = -\text{det} \begin{pmatrix} 2 & 3 \ 2 & 1 \end{pmatrix} = -(2\cdot1 - 3\cdot2) = 4$
- $C_{31} = \text{det} \begin{pmatrix} 3 & 1 \ 1 & -1 \end{pmatrix} = 3\cdot(-1) - 1\cdot1 = -4$
- $C_{32} = -\text{det} \begin{pmatrix} 2 & 1 \ 2 & -1 \end{pmatrix} = -(2(-1) - 1\cdot2) = 0$
- $C_{33} = \text{det} \begin{pmatrix} 2 & 3 \ 2 & 1 \end{pmatrix} = 2\cdot1 - 3\cdot2 = -4$
Die adjungierte Matrix ist dann:
$$ A^* = \begin{pmatrix} 3 & -6 & 0 \ -5 & 2 & 4 \ -4 & 0 & -4 \end{pmatrix} $$
- Inverse berechnen
Die Inverse einer Matrix berechnet sich mit der Formel: $$ A^{-1} = \frac{1}{\text{det}(A)} \cdot A^* $$ Da $\text{det}(A) = -14$, erhalten wir:
$$ A^{-1} = \frac{1}{-14} \cdot \begin{pmatrix} 3 & -6 & 0 \ -5 & 2 & 4 \ -4 & 0 & -4 \end{pmatrix} $$
Das endgültige Ergebnis ist: $$ A^{-1} = \begin{pmatrix} -\frac{3}{14} & \frac{6}{14} & 0 \ \frac{5}{14} & -\frac{2}{14} & -\frac{4}{14} \ \frac{4}{14} & 0 & \frac{4}{14} \end{pmatrix} $$
$$ A^{-1} = \begin{pmatrix} -\frac{3}{14} & \frac{3}{7} & 0 \ \frac{5}{14} & -\frac{1}{7} & -\frac{2}{7} \ \frac{2}{7} & 0 & \frac{2}{7} \end{pmatrix} $$
More Information
Die Inverse einer Matrix ist wichtig, um Gleichungssysteme zu lösen und um Transformationen im Raum durchzuführen. Eine Matrix hat nur dann eine Inverse, wenn ihre Determinante ungleich null ist.
Tips
- Den Fehler zu machen, die Determinante falsch zu berechnen.
- Zu vergessen, die Adjunkte richtig zu berechnen, insbesondere die Vorzeichen der Cofaktoren.
AI-generated content may contain errors. Please verify critical information