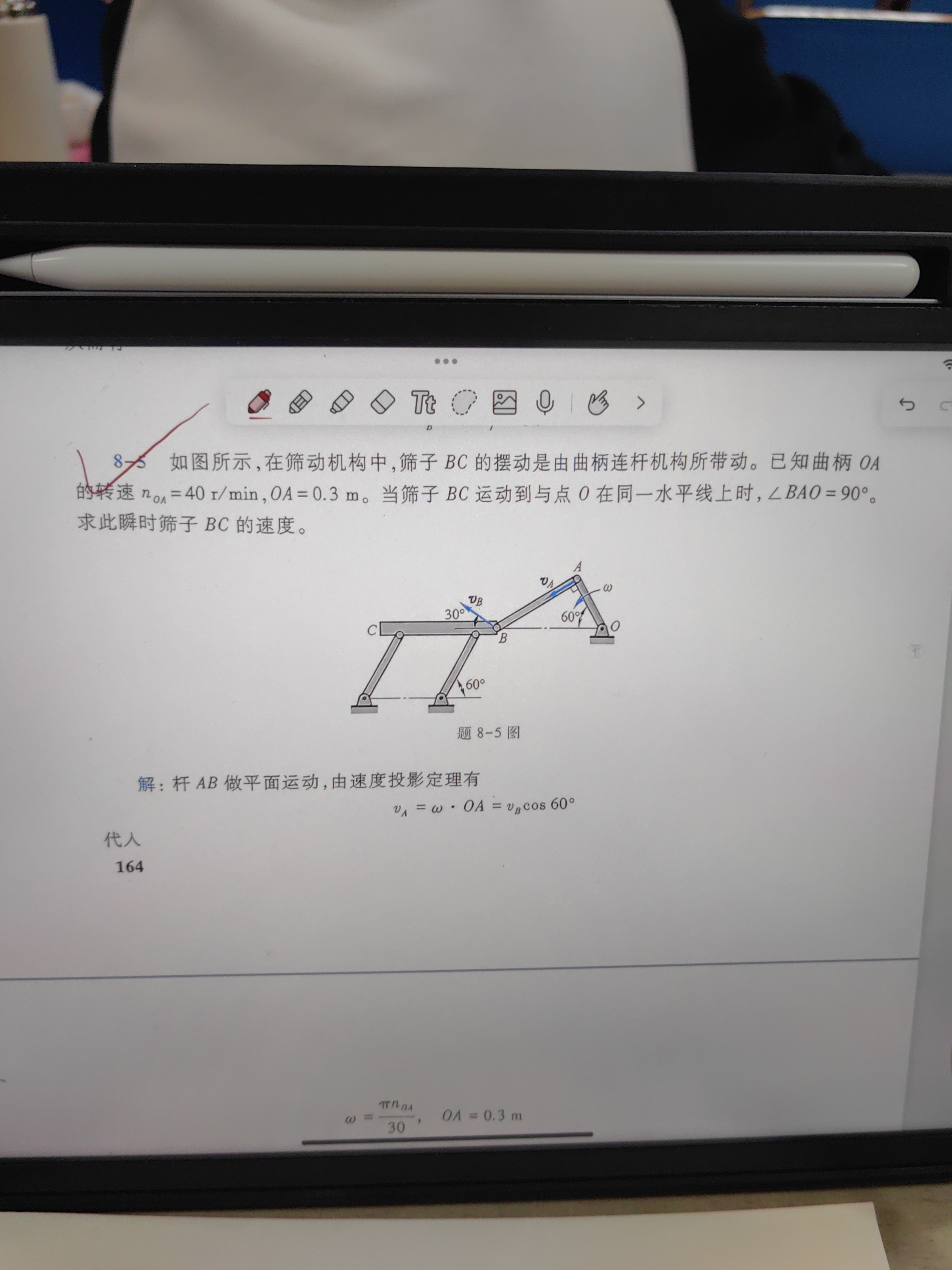
如图所示,在动机构中,杆子 BC 的摆动是由曲杆连接所驱动。已知杆 OA 的速度为 40 m/min,OA = 0.3 m。当杆子 BC 运移动到与点 O 在同一水平线上时,∠BAO = 90°,求此瞬时杆子 BC 的速度。 如图所示,在动机构中,杆子 BC 的摆动是由曲杆连接所驱动。已知杆 OA 的速度为 40 m/min,OA = 0.3 m。当杆子 BC 运移动到与点 O 在同一水平线上时,∠BAO = 90°,求此瞬时杆子 BC 的速度。
Understand the Problem
问题涉及一个机械系统中,杆件 BC 的运动速度与杆件 OA 的长度和角度有关。我们需要根据给定的速度和几何条件,计算杆件 BC 在某一时刻的速度。
Answer
杆件 BC 的速度为 $v_{BC} = 0.0157 \, \text{m/min}$。
Answer for screen readers
杆件 BC 的速度为 $v_{BC} = 0.0157 , \text{m/min}$。
Steps to Solve
- 确定已知量
给定的数据包括杆件 OA 的长度 $OA = 0.3 , \text{m}$,杆件 A 的角速度 $\omega = \frac{\pi}{30} , \text{rad/min}$,以及杆件 AB 运动的线速度 $v_A = 40 , \text{m/min}$。
- 计算杆件 A 的速度
根据速度关系,杆件 A 的速度可以用以下公式计算: $$v_A = \omega \cdot OA$$ 代入已知值: $$v_A = \frac{\pi}{30} \cdot 0.3$$
- 计算杆件 A 速度的实际值
计算得到杆件 A 的线速度: $$v_A = \frac{\pi}{30} \cdot 0.3 \approx 0.0314 , \text{m/min}$$
- 用几何关系找出速度 BC 的关系
根据三角函数,杆件 BC 的速度 $v_{BC}$ 可以表示为: $$v_{BC} = v_A \cdot \cos(60^\circ)$$
- 计算杆件 BC 的速度
代入计算结果: $$v_{BC} = 0.0314 \cdot \cos(60^\circ) = 0.0314 \cdot 0.5 = 0.0157 , \text{m/min}$$
杆件 BC 的速度为 $v_{BC} = 0.0157 , \text{m/min}$。
More Information
该问题涉及机械工程中杆件的运动分析,通过几何角度和速度关系可以计算不同杆件的线速度。这样的分析在设计和优化机械系统时非常重要。
Tips
- 忽视三角函数的应用,尤其是在涉及与角度相关的速度分量时。确保正确应用余弦和正弦函数。
- 在计算单元中不统一单位,例如将速度单位混用。确保所有单位一致。
AI-generated content may contain errors. Please verify critical information