Assume that f is a differentiable function. Find the elasticity of the following: a. x^5 f(x) b. (f(x))^(3/2)

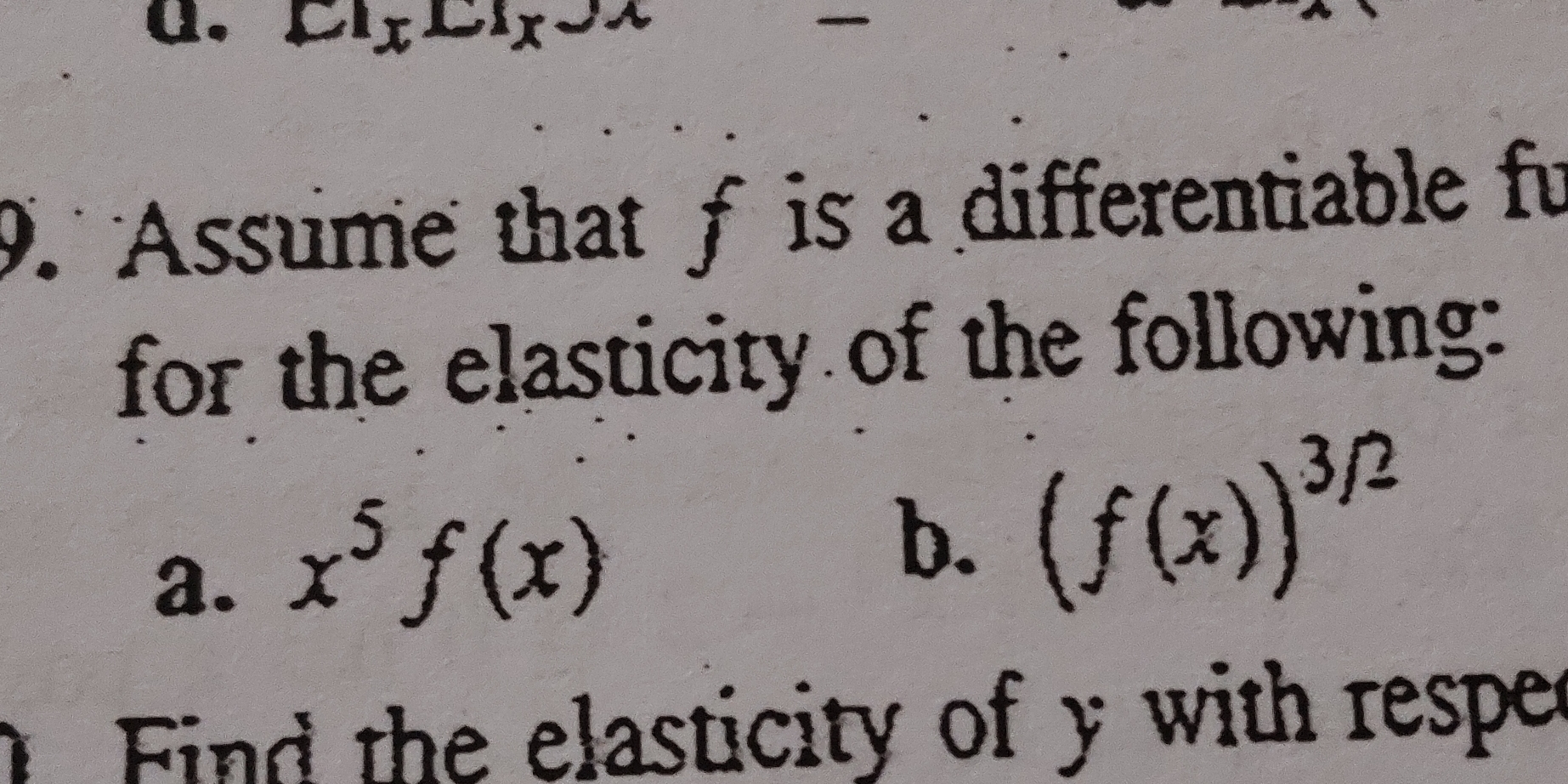
Understand the Problem

The question is asking to find the elasticity of two mathematical expressions involving a differentiable function f. The user wants to determine how the change in the function is related to the change in its variables for these specific cases.

Answer

a. $ E = \frac{5}{x} + \frac{f'(x)}{f(x)} $ b. $ E = \frac{3}{2} \frac{f'(x)}{f(x)} \cdot x $

Steps to Solve

Understanding Elasticity Elasticity measures how a function responds to changes in its variables. For a function ( g(x) ), the elasticity ( E ) is given by: $$ E = \frac{d(g)}{d(x)} \cdot \frac{x}{g(x)} $$
Finding Elasticity of ( x^5 f(x) ) Let ( g(x) = x^5 f(x) ).
- Differentiate ( g(x) ) using the product rule: $$ g'(x) = 5x^4 f(x) + x^5 f'(x) $$
- Now compute elasticity: $$ E = \left(5x^4 f(x) + x^5 f'(x)\right) \cdot \frac{x}{x^5 f(x)} = \frac{(5x^4 f(x) + x^5 f'(x)) \cdot x}{x^5 f(x)} $$ Simplifying this gives: $$ E = \frac{5}{x} + \frac{f'(x)}{f(x)} $$
Finding Elasticity of ( (f(x))^{3/2} ) Let ( h(x) = (f(x))^{3/2} ).
- Differentiate ( h(x) ) using the chain rule: $$ h'(x) = \frac{3}{2}(f(x))^{1/2} \cdot f'(x) $$
- Now compute elasticity: $$ E = \left(\frac{3}{2}(f(x))^{1/2} f'(x)\right) \cdot \frac{x}{(f(x))^{3/2}} = \frac{3}{2} \frac{f'(x)}{f(x)} \cdot x $$

a. The elasticity of ( x^5 f(x) ) is ( E = \frac{5}{x} + \frac{f'(x)}{f(x)} ).

b. The elasticity of ( (f(x))^{3/2} ) is ( E = \frac{3}{2} \frac{f'(x)}{f(x)} \cdot x ).

More Information

Elasticity helps in understanding how sensitive a function is to changes in its input. In economic terms, it reflects how demand responds to price changes.

Tips

Forgetting to apply the product or chain rule correctly when differentiating.
Not simplifying the final elasticity expression.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!