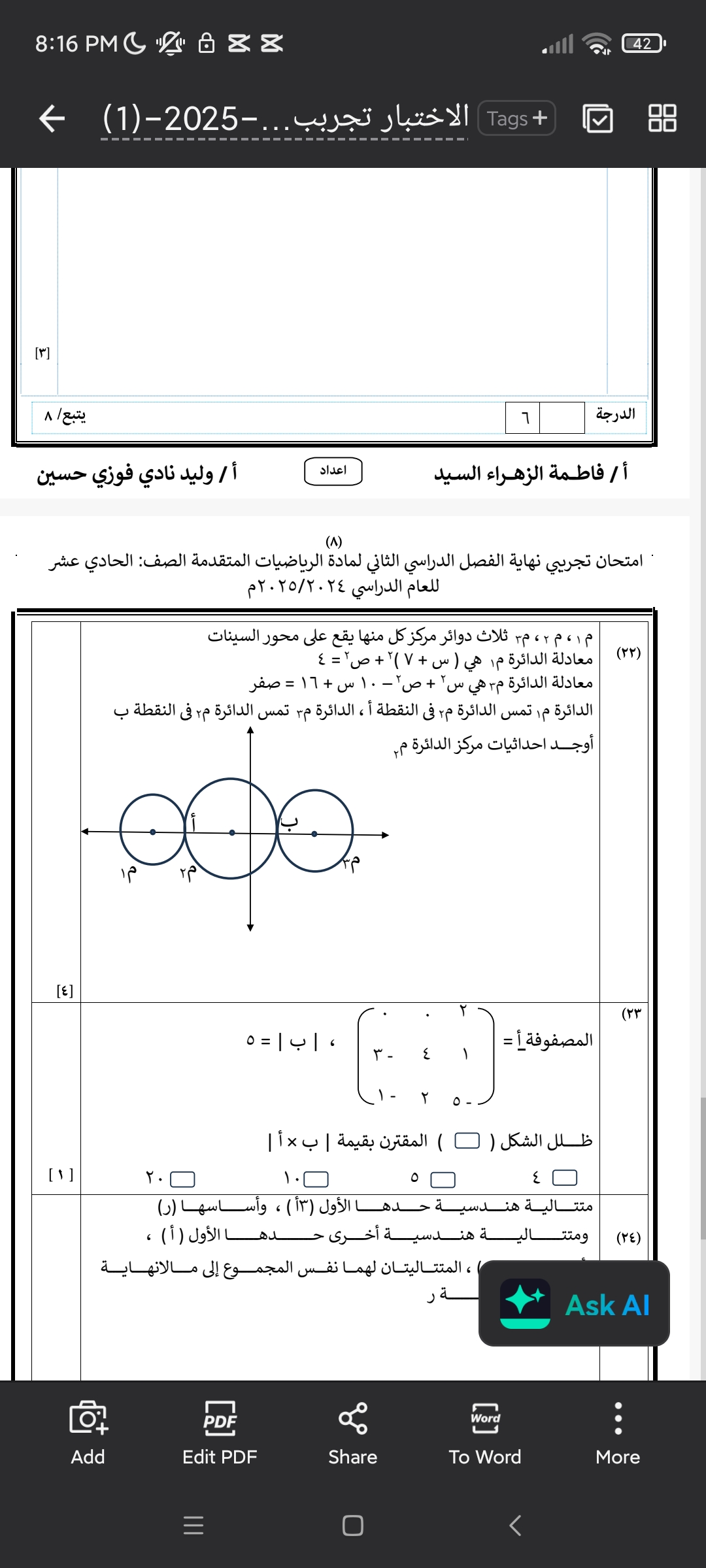
أوجد إحداثيات مركز الدائرة.

Steps to Solve

1. فهم المعطيات تم إعطاؤنا ثلاث دوائر، كل منها تقع على محور السينات (x-axis) بمراكز معروفة. يجب أن نجد إحداثيات مركز دائرة أخرى (دائرة ٣) تلامس هذه الدوائر.

2. تحديد مراكز الدوائر الأولى والثانية لنبدأ بتحديد إحداثيات مراكز الدوائر الأخرى.

• مركز الدائرة 1 هو ( (1, 4) ).
• مركز الدائرة 2 هو ( (3, 4) ).

3. تحديد نظرية التلامس عند تلامس الدوائر، فإن المسافة بين مراكزها تساوي مجموع أنصاف أقطارها. لدينا:

• نصف قطر الدائرة 1 هو ( 1 ) (لأن الدائرة 1 تقع على المحور).
• نصف قطر الدائرة 2 هو ( 1 ) (نفس المنطق).

إذاً، المسافة بين الدائرة 1 والدائرة 2 هي ( 1 + 1 = 2 ).

4. تحديد مركز الدائرة ٣ لإيجاد إحداثيات مركز الدائرة ٣، نضع أن المركز سيكون على نفس الاستقامة (المستوى الأفقي)، أي:

$$ y = 4 $$

لذا يصبح لدينا: $$ x_3 - x_1 = r_1 + r_3 $$ $$ x_3 - 1 = 1 + r_3 $$

5. تحديد نصف قطر الدائرة ٣ لنفرض أن نصف قطر الدائرة ٣ هو ( r_3 ). إذاً، يجب أن نختار ( r_3 = 1 ) كما فعلنا في الدائرتين الأخريتين.

6. حل المعادلة نعود إلى المعادلة: $$ x_3 - 1 = 1 + 1 $$ $$ x_3 - 1 = 2 $$ $$ x_3 = 3 $$

7. إحداثيات مركز الدائرة ٣ إذن، إحداثيات مركز الدائرة ٣ هي:

$$ (3, 4) $$