Analyze the properties of the lines and points in the coordinate plane provided.
Understand the Problem
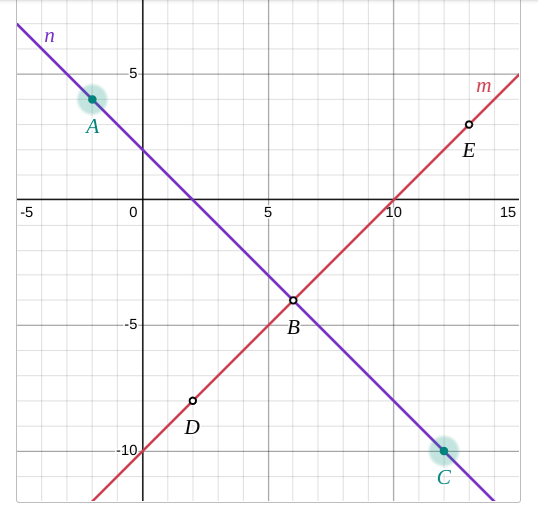
The image shows a coordinate plane with two lines, labeled 'n' and 'm', intersecting at a point B. Several other points are marked on or near these lines (A, C, D, and E). The user likely has a question about the properties of these lines, such as finding the equation, the slope, or angles etc.
Answer
$y = -\frac{6}{5}x + 4$
Answer for screen readers
The equation of line $n$ is: $y = -\frac{6}{5}x + 4$
Steps to Solve
- Identify coordinates of points on line n
From the image, line $n$ appears to pass through points $A$ and $C$. Approximate coordinates: $A = (0, 4)$ and $C = (10, -8)$.
- Calculate the slope of line n
The slope $m$ of a line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by: $m = \frac{y_2 - y_1}{x_2 - x_1}$
In our case, $(x_1, y_1) = (0, 4)$ and $(x_2, y_2) = (10, -8)$. $m = \frac{-8 - 4}{10 - 0} = \frac{-12}{10} = -\frac{6}{5}$
- Determine the y-intercept of line n
The y-intercept is the point where the line crosses the y-axis (x=0). From point $A = (0, 4)$ it is easy to see that the line crosses the y-axis at $y = 4$. Call this value $b$.
- Write the equation of line n in slope-intercept form
The slope-intercept form of a line is $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. Substituting the values we have: $y = -\frac{6}{5}x + 4$
The equation of line $n$ is: $y = -\frac{6}{5}x + 4$
More Information
The slope of line $n$ is negative, which means the line goes downwards as $x$ increases. The $y$-intercept is positive, indicating where the line crosses the vertical axis.
Tips
A common mistake is misreading the coordinates of the points from the graph. It's important to carefully observe the grid and estimate the coordinates as accurately as possible. Another mistake includes incorrectly calculating the slope or y-intercept using the coordinates. Finally, there might be mistakes in substituting the values in the slope-intercept form.
AI-generated content may contain errors. Please verify critical information