Analyze the electrical circuit.
Understand the Problem
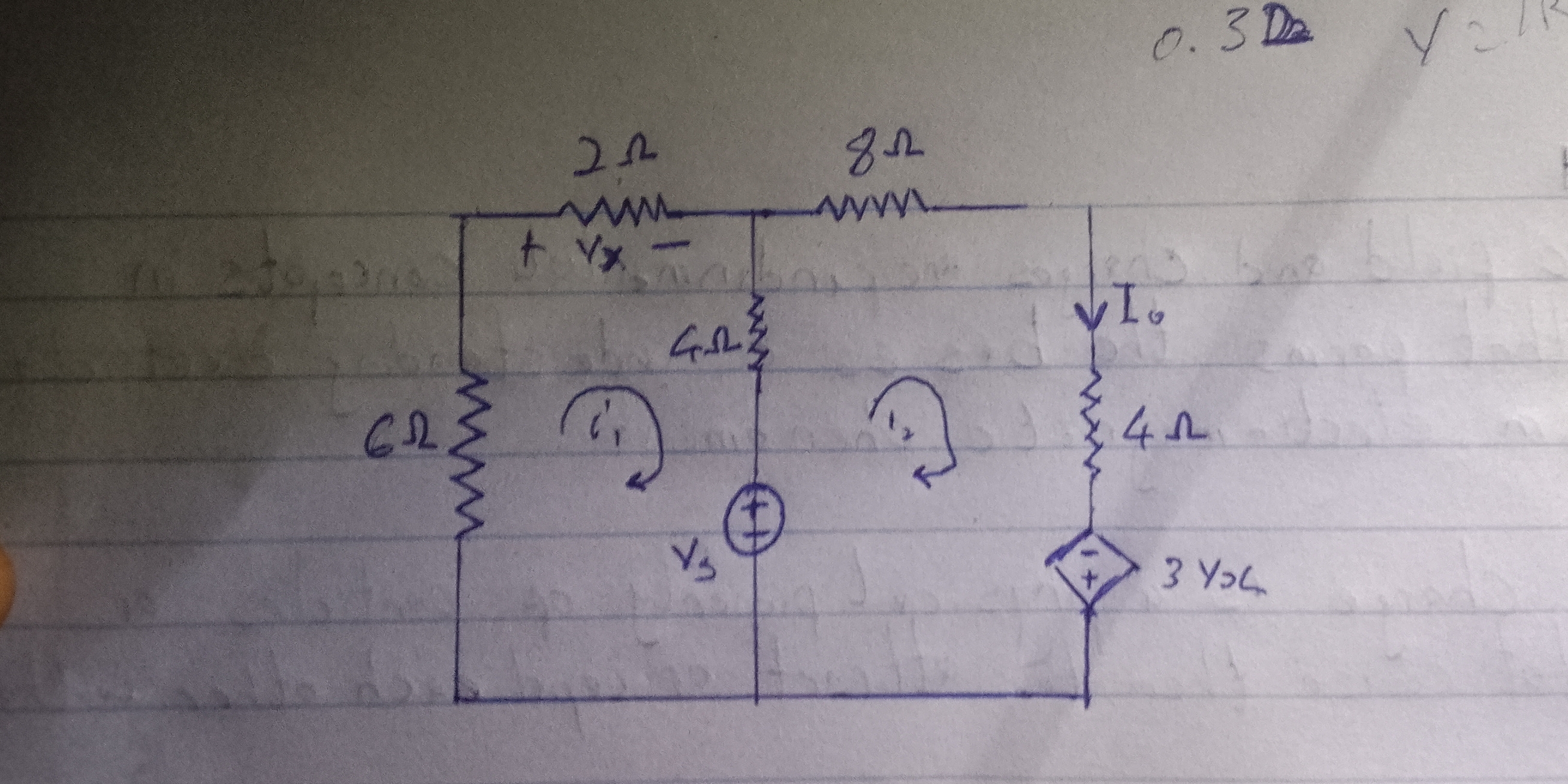
The question presents an electrical circuit diagram containing resistors, current sources, and dependent voltage sources. It implicitly asks for an analysis or solution of the circuit, which would likely involve determining currents, voltages, or power values within the circuit. This requires knowledge of circuit analysis techniques like mesh analysis, nodal analysis, or source transformation, along with Ohm's law and Kirchhoff's laws.
Answer
$I_o = 0$
Answer for screen readers
$I_o = 0$
Steps to Solve
- Apply Mesh Analysis
Apply mesh analysis to the circuit. Define two mesh currents, $i_1$ and $i_2$, as given in the diagram.
- Write KVL equation for Mesh 1
Apply Kirchhoff's Voltage Law (KVL) around mesh 1:
$ -V_s + 6i_1 +2i_1 + V_x = 0 $ $V_x = 2i_1$
Substitute $ V_x $: $ -V_s + 6i_1 + 2i_1 + 2i_1 = 0 $ $ -V_s + 10i_1 = 0 $ $ V_s = 10i_1 $
- Write KVL equation for Mesh 2
Apply Kirchhoff's Voltage Law (KVL) around mesh 2:
$ -V_x + 8i_2 + 4i_2 + 3V_x = 0 $ $ 2V_x + 12i_2 = 0 $ $ V_x = -6i_2 $
- Relate Mesh Currents
Note that $V_s$ (the current source) is defined as $ i_2 - i_1 $.
$ V_s = i_2 - i_1 $
- Solve the System of Equations
We have the following equations:
$ V_s = 10i_1 $ $ V_x = 2i_1 $ $ V_x = -6i_2 $ $ V_s = i_2 - i_1 $
From $ V_x = 2i_1 $ and $ V_x = -6i_2 $, we have $ 2i_1 = -6i_2 $ or $ i_1 = -3i_2 $. Substitute into $ V_s = 10i_1 $ to get $ V_s = -30i_2 $. Substitute into $ V_s = i_2 - i_1 $ to get $ V_s = i_2 - (-3i_2) = 4i_2 $. Therefore $ 4i_2 = -30i_2 $, implying that $ 34i_2 = 0 $, and so $ i_2 = 0 $. Then $ i_1 = -3i_2 = 0 $, and $ V_s = 4i_2 = 0 $. Also $ V_x = 2i_1 = 0 $
- Calculate $I_o$
$I_o$ flows through the $4 \Omega$ resistor in the second mesh. The voltage across this resistor is 3$V_x = 0$. Therefore, $I_o = \frac{0}{4} = 0$.
$I_o = 0$
More Information
The current $I_o$ is zero because the dependent voltage source $3V_x$ is zero, which is a result of the circuit's configuration leading to zero mesh currents.
Tips
A common mistake is to incorrectly apply KVL or KCL, especially around the dependent sources. Additionally, errors can be made when substituting and simplifying the equations. Pay close attention to the polarity of voltage drops across resistors and the directions of current flow.
AI-generated content may contain errors. Please verify critical information