احتمال A وارده بر A U B
Understand the Problem
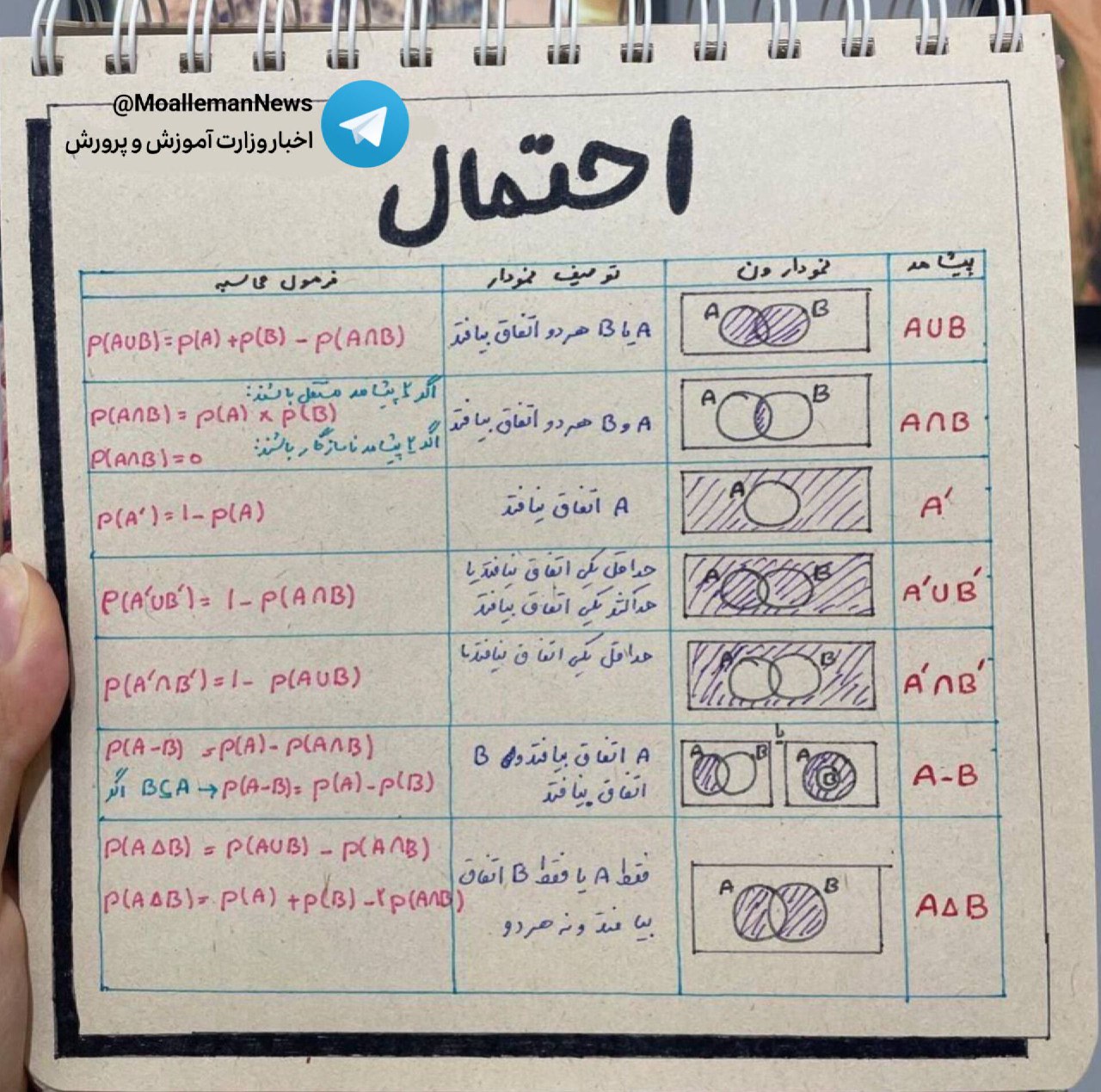
سوال مربوط به احتمال و فرمولهای آن در ریاضیات است. این سوال به بررسی روابط بین مجموعههای A و B و احتمال وقوع آنها میپردازد.
Answer
فرمولهای احتمال برای دو مجموعه A و B عبارتند از: $$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$ و $$ P(A - B) = P(A) - P(A \cap B) $$
Answer for screen readers
فرمولهای احتمال برای مجموعههای A و B به شرح زیر است: $$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$ $$ P(A') = 1 - P(A) $$ $$ P(A - B) = P(A) - P(A \cap B) $$
Steps to Solve
-
درک مفاهیم پایه احتمال برای حل این سوال، باید فرمولهای مربوط به احتمال و مفاهیم مجموعهها را درک کنیم. مجموعهها A و B میتوانند با استفاده از فرمولهای زیر ارتباط داشته باشند.
-
استفاده از فرمولهای احتمال برای دو رویداد A و B، فرمول اصلی احتمال به صورت زیر است: $$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$ این فرمول رابطه بین احتمال اتحاد دو مجموعه و احتمال تداخل آنها را بیان میکند.
-
محاسبه احتمال مکمل برای محاسبه احتمال مکمل یک مجموعه، از فرمول زیر استفاده میکنیم: $$ P(A') = 1 - P(A) $$ که در آن $A'$ مکمل مجموعه A است.
-
محاسبه احتمال تداخل احتمال تداخل دو مجموعه به صورت زیر محاسبه میشود: $$ P(A \cap B) = P(A) + P(B) - P(A \cup B) $$ این فرمول میتواند در زمانی که احتمال اتحاد و احتمال یکی از رویدادها را داریم استفاده شود.
-
محاسبه احتمال تفاضل برای یافتن احتمال تفاضل دو مجموعه، از فرمول زیر استفاده میکنیم: $$ P(A - B) = P(A) - P(A \cap B) $$ با این کار احتمال A را بدون قسمت مشترک آن با B محاسبه میکنیم.
فرمولهای احتمال برای مجموعههای A و B به شرح زیر است: $$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$ $$ P(A') = 1 - P(A) $$ $$ P(A - B) = P(A) - P(A \cap B) $$
More Information
این فرمولها پایه و اساس مباحث احتمال و آمار هستند. در زندگی روزمره، این مفاهیم برای تحلیل و پیشبینی رفتارهای تصادفی بسیار کاربردیاند.
Tips
- غلط در استفاده از فرمول مکمل: اطمینان حاصل کنید که مکمل را به درستی محاسبه کنید. احتمال مکمل همیشه به صورت $1 - P(A)$ است.
- عدم توجه به احتمال تداخل: هنگام محاسبه احتمال اتحاد، فراموش نکنید که احتمال تداخل را کم کنید.
AI-generated content may contain errors. Please verify critical information