Add the two expressions: x/(x^2 - 5x - 6) + (x-6)/(x+1)
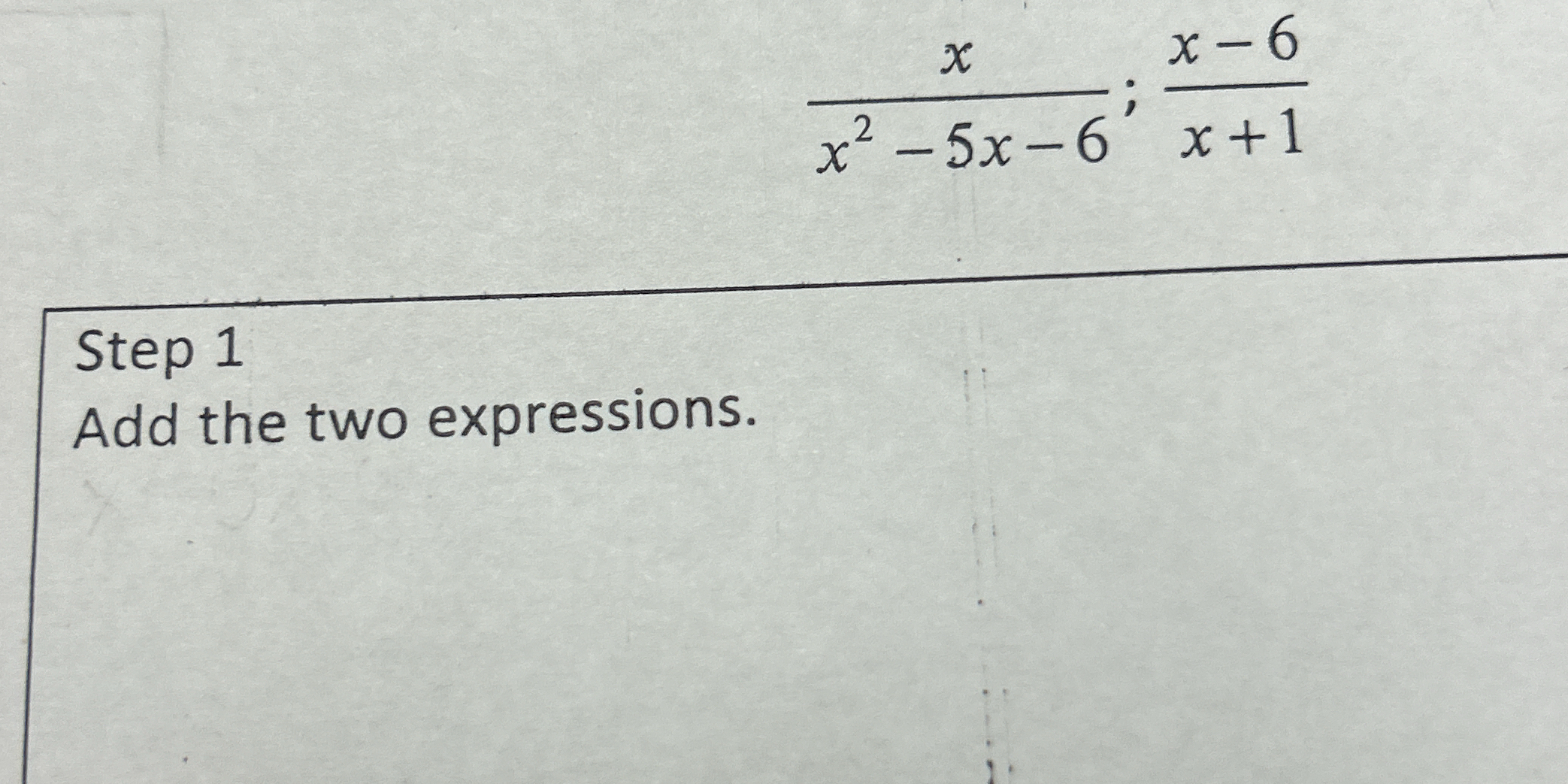
Understand the Problem
The question is asking to add two rational expressions. We will factor the denominator of the first expression, find a common denominator, and then add the numerators.
Answer
$\frac{x^2 - 11x + 36}{(x-6)(x+1)}$
Answer for screen readers
$\frac{x^2 - 11x + 36}{(x-6)(x+1)}$
Steps to Solve
- Rewrite the problem
The problem is to add the two rational expressions, which can be written as: $$ \frac{x}{x^2 - 5x - 6} + \frac{x-6}{x+1} $$
- Factor the denominator of the first expression
We factor $x^2 - 5x - 6$ into $(x-6)(x+1)$. So the expression becomes: $$ \frac{x}{(x-6)(x+1)} + \frac{x-6}{x+1} $$
- Find a common denominator
The common denominator is $(x-6)(x+1)$. We need to multiply the second term by $\frac{x-6}{x-6}$: $$ \frac{x}{(x-6)(x+1)} + \frac{(x-6)(x-6)}{(x+1)(x-6)} $$
- Expand the numerator of the second term
Expanding $(x-6)(x-6)$ gives $x^2 - 12x + 36$. The expression is now: $$ \frac{x}{(x-6)(x+1)} + \frac{x^2 - 12x + 36}{(x-6)(x+1)} $$
- Add the numerators
Add the numerators together over the common denominator: $$ \frac{x + x^2 - 12x + 36}{(x-6)(x+1)} = \frac{x^2 - 11x + 36}{(x-6)(x+1)} $$
- Check if the numerator can be factored
The numerator $x^2 - 11x + 36$ cannot be factored using integers.
- Final Answer
The final simplified expression is: $$ \frac{x^2 - 11x + 36}{(x-6)(x+1)} $$
$\frac{x^2 - 11x + 36}{(x-6)(x+1)}$
More Information
The expression cannot be simplified further because the quadratic in the numerator does not factor nicely, and there are no common factors in the numerator and denominator.
Tips
A common mistake is to incorrectly factor the quadratic in the denominator or to make an error when expanding $(x-6)(x-6)$. Another common mistake is to forget to multiply both the numerator and denominator of the second term by $(x-6)$ when finding the common denominator.
AI-generated content may contain errors. Please verify critical information