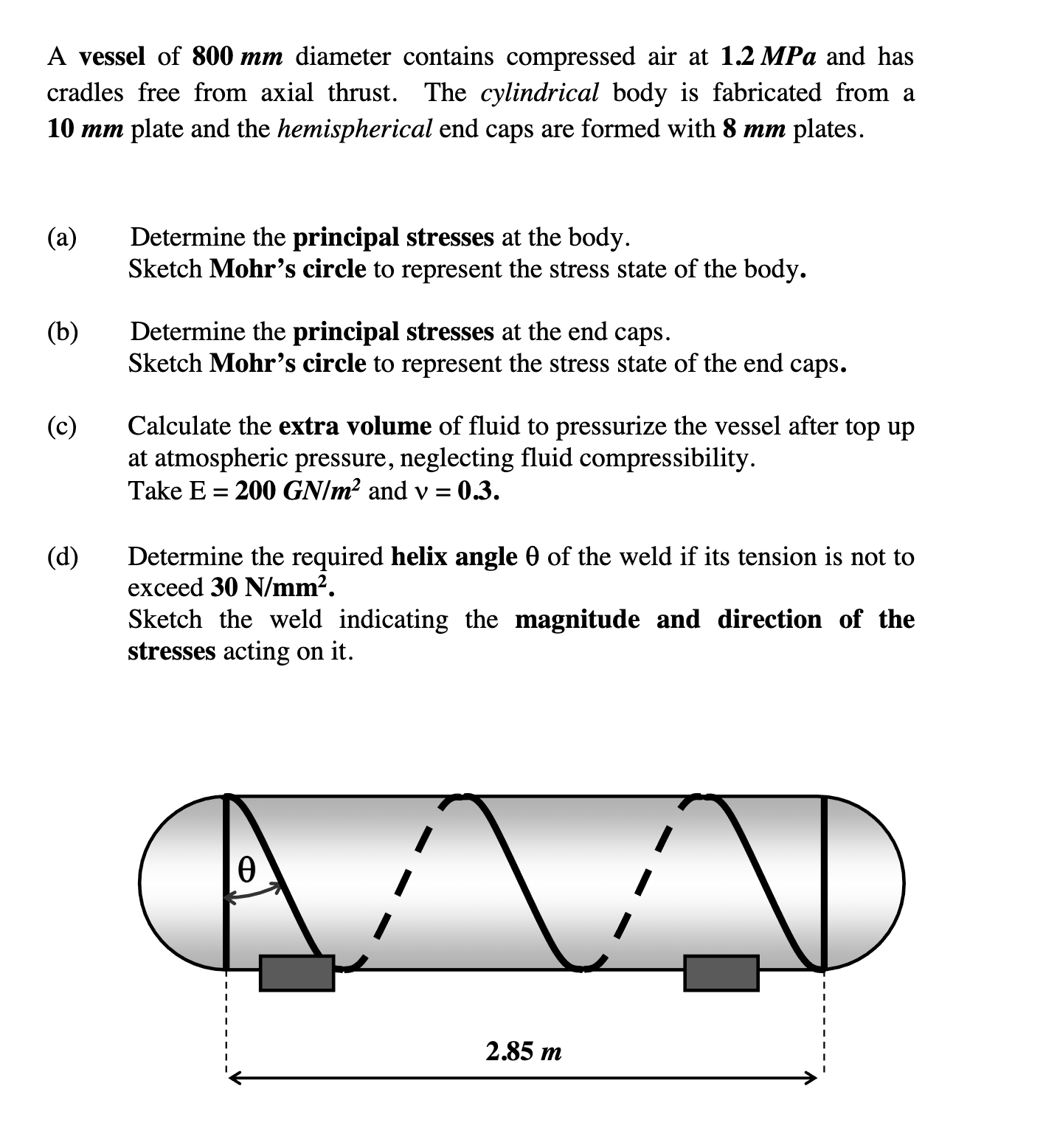
A vessel of 800 mm diameter contains compressed air at 1.2 MPa and has cradles free from axial thrust. The cylindrical body is fabricated from a 10 mm plate and the hemispherical e... A vessel of 800 mm diameter contains compressed air at 1.2 MPa and has cradles free from axial thrust. The cylindrical body is fabricated from a 10 mm plate and the hemispherical end caps are formed with 8 mm plates. (a) Determine the principal stresses at the body. Sketch Mohr's circle to represent the stress state of the body. (b) Determine the principal stresses at the end caps. Sketch Mohr's circle to represent the stress state of the end caps. (c) Calculate the extra volume of fluid to pressurize the vessel after top up at atmospheric pressure, neglecting fluid compressibility. Take E = 200 GN/m² and v = 0.3. (d) Determine the required helix angle 0 of the weld if its tension is not to exceed 30 N/mm². Sketch the weld indicating the magnitude and direction of the stresses acting on it. Read more

Steps to Solve

1. Calculate the principal stresses in the cylindrical body

The principal stresses in a cylindrical pressure vessel are the hoop stress ($\sigma_h$) and the longitudinal stress ($\sigma_l$). These can be calculated using the following formulas:

Hoop stress: $$ \sigma_h = \frac{p \cdot r}{t} $$ Longitudinal stress: $$ \sigma_l = \frac{p \cdot r}{2t} $$ where $p$ is the internal pressure, $r$ is the radius of the vessel, and $t$ is the thickness of the cylindrical body.

Given: $p = 1.2 \text{ MPa} = 1.2 \text{ N/mm}^2$ $r = 800 \text{ mm} / 2 = 400 \text{ mm}$ $t = 10 \text{ mm}$

$$ \sigma_h = \frac{1.2 \cdot 400}{10} = 48 \text{ N/mm}^2 = 48 \text{ MPa} $$ $$ \sigma_l = \frac{1.2 \cdot 400}{2 \cdot 10} = 24 \text{ N/mm}^2 = 24 \text{ MPa} $$ The principal stresses are $\sigma_1 = \sigma_h = 48 \text{ MPa}$ and $\sigma_2 = \sigma_l = 24 \text{ MPa}$. The third principal stress is $\sigma_3 = 0 \text{ MPa}$ (atmospheric pressure on the outside).

2. Sketch Mohr's circle for the cylindrical body

Mohr's circle is a graphical representation of the stress state. For the cylindrical body, the center of the circle is at $(\frac{\sigma_1 + \sigma_2}{2}, 0) = (\frac{48 + 24}{2}, 0) = (36, 0)$. The radius of the circle is $R = \frac{\sigma_1 - \sigma_2}{2} = \frac{48 - 24}{2} = 12$. The circle is plotted with the center at (36,0) and radius of 12, representing the stress state.

3. Calculate the principal stresses in the hemispherical end caps

For a hemispherical end cap, the principal stresses are equal in all directions and can be calculated as: $$ \sigma = \frac{p \cdot r}{2t} $$

Given: $p = 1.2 \text{ MPa} = 1.2 \text{ N/mm}^2$ $r = 400 \text{ mm}$ $t = 8 \text{ mm}$

$$ \sigma = \frac{1.2 \cdot 400}{2 \cdot 8} = 30 \text{ N/mm}^2 = 30 \text{ MPa} $$ The principal stresses are $\sigma_1 = \sigma_2 = 30 \text{ MPa}$. The third principal stress is $\sigma_3 = 0 \text{ MPa}$.

4. Sketch Mohr's circle for the end caps

For the end caps, since $\sigma_1 = \sigma_2 = 30 \text{ MPa}$, Mohr's circle is simply a point at (30, 0). This represents a biaxial stress state with equal stresses.

5. Calculate the extra volume required for pressurization

The extra volume required can be calculated from the volumetric strain. First, calculate the strains in the cylindrical body: $$ \epsilon_h = \frac{1}{E} (\sigma_h - \nu \sigma_l) = \frac{1}{200 \times 10^3} (48 - 0.3 \cdot 24) = \frac{40.8}{200 \times 10^3} = 2.04 \times 10^{-4} $$ $$ \epsilon_l = \frac{1}{E} (\sigma_l - \nu \sigma_h) = \frac{1}{200 \times 10^3} (24 - 0.3 \cdot 48) = \frac{9.6}{200 \times 10^3} = 0.48 \times 10^{-4} $$ The volumetric strain is $\epsilon_v = \epsilon_h + \epsilon_h + \epsilon_l = 2\epsilon_h + \epsilon_l = 2(2.04 \times 10^{-4}) + 0.48 \times 10^{-4} = 4.08 \times 10^{-4} + 0.48 \times 10^{-4} = 4.56 \times 10^{-4}$.

The volume of the cylindrical part of the vessel is $$ V_{cylinder} = \pi r^2 l = \pi (0.4 \text{ m})^2 (2.85 \text{ m}) = \pi \cdot 0.16 \cdot 2.85 = 1.4325 \text{ m}^3 $$ The volume of each hemispherical end cap is $V_{cap} = \frac{2}{3} \pi r^3 = \frac{2}{3} \pi (0.4 \text{ m})^3 = \frac{2}{3} \pi (0.064) = 0.134 \text{ m}^3$. The total volume of the two end caps is $2V_{cap} = 2(0.134) = 0.268 \text{ m}^3$. The total volume of the vessel is $V = V_{cylinder} + 2V_{cap} = 1.4325 + 0.268 = 1.7005 \text{ m}^3$ The extra volume required is $\Delta V = V \epsilon_v = 1.7005 \text{ m}^3 \cdot 4.56 \times 10^{-4} = 0.000775 \text{ m}^3 = 775 \times 10^{-6} \text{ m}^3 = 775 \text{ cm}^3 = 0.775 \text{ liters}$.

6. Determine the required helix angle

The normal stress on the weld ($\sigma_n$) can be expressed in terms of the hoop stress ($\sigma_h$) and longitudinal stress ($\sigma_l$) as: $$ \sigma_n = \sigma_h \sin^2(\theta) + \sigma_l \cos^2(\theta) $$ where $\theta$ is the helix angle. The tension on the weld must not exceed 30 N/mm², so $\sigma_n \leq 30 \text{ MPa}$. We have $\sigma_h = 48 \text{ MPa}$ and $\sigma_l = 24 \text{ MPa}$. Therefore: $$ 30 = 48 \sin^2(\theta) + 24 \cos^2(\theta) $$ Since $\cos^2(\theta) = 1 - \sin^2(\theta)$: $$ 30 = 48 \sin^2(\theta) + 24 (1 - \sin^2(\theta)) $$ $$ 30 = 48 \sin^2(\theta) + 24 - 24 \sin^2(\theta) $$ $$ 6 = 24 \sin^2(\theta) $$ $$ \sin^2(\theta) = \frac{6}{24} = \frac{1}{4} $$ $$ \sin(\theta) = \frac{1}{2} $$ $$ \theta = \arcsin\left(\frac{1}{2}\right) = 30^\circ $$ The required helix angle is 30 degrees. The stresses acting on the weld are the hoop and longitudinal stresses, oriented with respect to the weld angle.