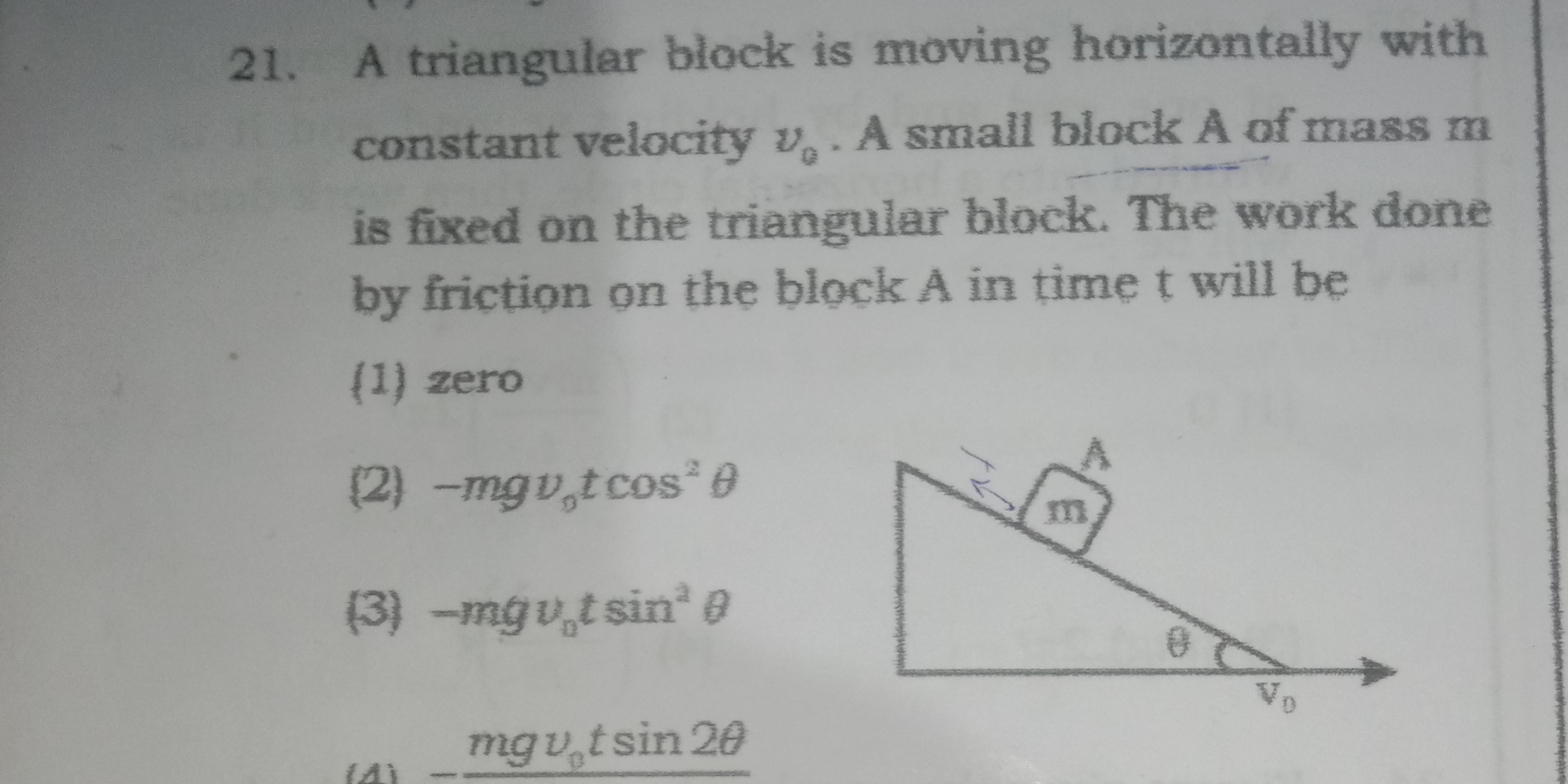
A triangular block is moving horizontally with constant velocity v0. A small block A of mass m is fixed on the triangular block. The work done by friction on the block A in time t... A triangular block is moving horizontally with constant velocity v0. A small block A of mass m is fixed on the triangular block. The work done by friction on the block A in time t will be?
Understand the Problem
The question asks to calculate the work done by friction on a small block A of mass m, which is placed on a triangular block that is moving horizontally with a constant velocity. The work needs to be expressed in terms of given variables and constants over a time period t.
Answer
The work done by friction on the block A in time $t$ is: $$ W = mg v_0 t \sin \theta \cos \theta $$
Answer for screen readers
The work done by friction on the block A in time $t$ will be: $$ W = mg v_0 t \sin \theta \cos \theta $$
Steps to Solve
-
Identify the forces acting on block A Block A is affected by gravitational force ($mg$) acting downward, normal force ($N$) acting perpendicular to the surface, and frictional force ($F_f$) acting up the incline.
-
Determine the component of gravitational force parallel to the incline The component of gravitational force acting parallel to the incline can be calculated as: $$ F_{\text{gravity, parallel}} = mg \sin \theta $$
-
Identify the movement and consider acceleration Since the triangular block is moving with constant velocity, block A experiences no relative acceleration. Thus, the frictional force must balance the component of gravitational force along the incline. The work done by friction is what we're interested in.
-
Calculate the displacement of block A relative to the ground The horizontal distance covered by the block while the triangular block moves a distance $v_0 t$ is: $$ d = v_0 t \cos \theta $$
-
Express the work done by friction The work done by friction can be calculated by multiplying the frictional force by the distance moved in the direction of that force: $$ W = F_f \cdot d $$
-
Substituting the forces and distances Here, $F_f = mg \sin \theta$. Thus, substituting in: $$ W = (mg \sin \theta)(v_0 t \cos \theta) = mg v_0 t \sin \theta \cos \theta $$
The work done by friction on the block A in time $t$ will be: $$ W = mg v_0 t \sin \theta \cos \theta $$
More Information
The formula shows that the work done by friction depends on the mass, gravitational acceleration, the velocity of the base block, the angle of inclination, and the time period the block A is on the inclined surface. This relationship emphasizes the impact of both the gravitational force and the motion of the inclined block on the work done by friction.
Tips
- Forgetting to calculate the correct direction of forces: Always remember that friction acts against the direction of motion.
- Neglecting the component of forces along the incline: It's important to break down forces correctly, especially in inclined problems.
AI-generated content may contain errors. Please verify critical information