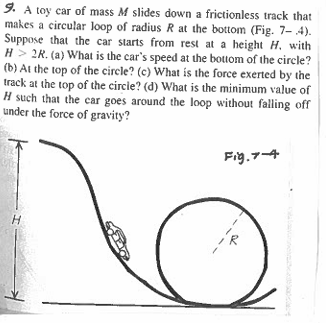
A toy car of mass M slides down a frictionless track that makes a circular loop of radius R at the bottom. Suppose that the car starts from rest at a height H, with H > 2R. (a) Wha... A toy car of mass M slides down a frictionless track that makes a circular loop of radius R at the bottom. Suppose that the car starts from rest at a height H, with H > 2R. (a) What is the car's speed at the bottom of the circle? (b) At the top of the circle? (c) What is the force exerted by the track at the top of the circle? (d) What is the minimum value of H such that the car goes around the loop without falling off under the force of gravity? Read more

Steps to Solve

1. Finding Speed at the Bottom of the Loop

To find the car's speed at the bottom of the loop, we can use the conservation of mechanical energy. The potential energy at height $H$ gets converted into kinetic energy at the bottom.

The potential energy at height $H$ is given by: $$ PE = Mgh $$

At the bottom of the loop, the kinetic energy is: $$ KE = \frac{1}{2}mv^2 $$

Setting the potential energy equal to the kinetic energy: $$ Mgh = \frac{1}{2}Mv^2 $$

2. Simplifying for Speed at the Bottom

We can cancel $M$ from both sides and rearrange to find the speed $v$: $$ gh = \frac{1}{2}v^2 $$

Multiplying both sides by 2 gives: $$ 2gh = v^2 $$

Taking the square root yields: $$ v = \sqrt{2gh} $$

3. Finding Speed at the Top of the Loop

Now, to find the speed at the top of the loop, we need to consider that the car has both kinetic and potential energy at that point. The height at the top is $2R$, and the energy conservation between the bottom and the top gives us:

$$ Mgh = \frac{1}{2}Mv_t^2 + Mg(2R) $$

This can be simplified to: $$ gh = \frac{1}{2}v_t^2 + 2gR $$

4. Solving for Speed at the Top

Rearranging this equation to solve for $v_t$: $$ \frac{1}{2}v_t^2 = gh - 2gR $$

Multiplying both sides by 2: $$ v_t^2 = 2gh - 4gR $$

Taking the square root, we find: $$ v_t = \sqrt{2gh - 4gR} $$

5. Finding the Force at the Top of the Circle

The force exerted by the track at the top of the loop is the centripetal force required to keep the car in circular motion plus the gravitational force acting on the car. The centripetal force needed is: $$ F_c = \frac{Mv_t^2}{R} $$

At the top, the weight of the car contributes to the centripetal force: $$ F_c = N + Mg $$

Where $N$ is the normal force exerted by the track.

So, we equate this: $$ N + Mg = \frac{Mv_t^2}{R} $$

Rearranging gives: $$ N = \frac{Mv_t^2}{R} - Mg $$

6. Finding Minimum Height for the Loop

For the car to just make it around the loop without falling off, the speed $v_t$ at the top must be enough to provide the required centripetal acceleration, which will be zero at the minimum height.

So we set: $$ v_t^2 = gR $$

Substituting into our earlier equation for $v_t$ gives: $$ 2gh - 4gR = gR $$

This simplifies to: $$ 2gh = 5gR $$

So, the minimum height $H$ required is: $$ H = \frac{5R}{2} $$