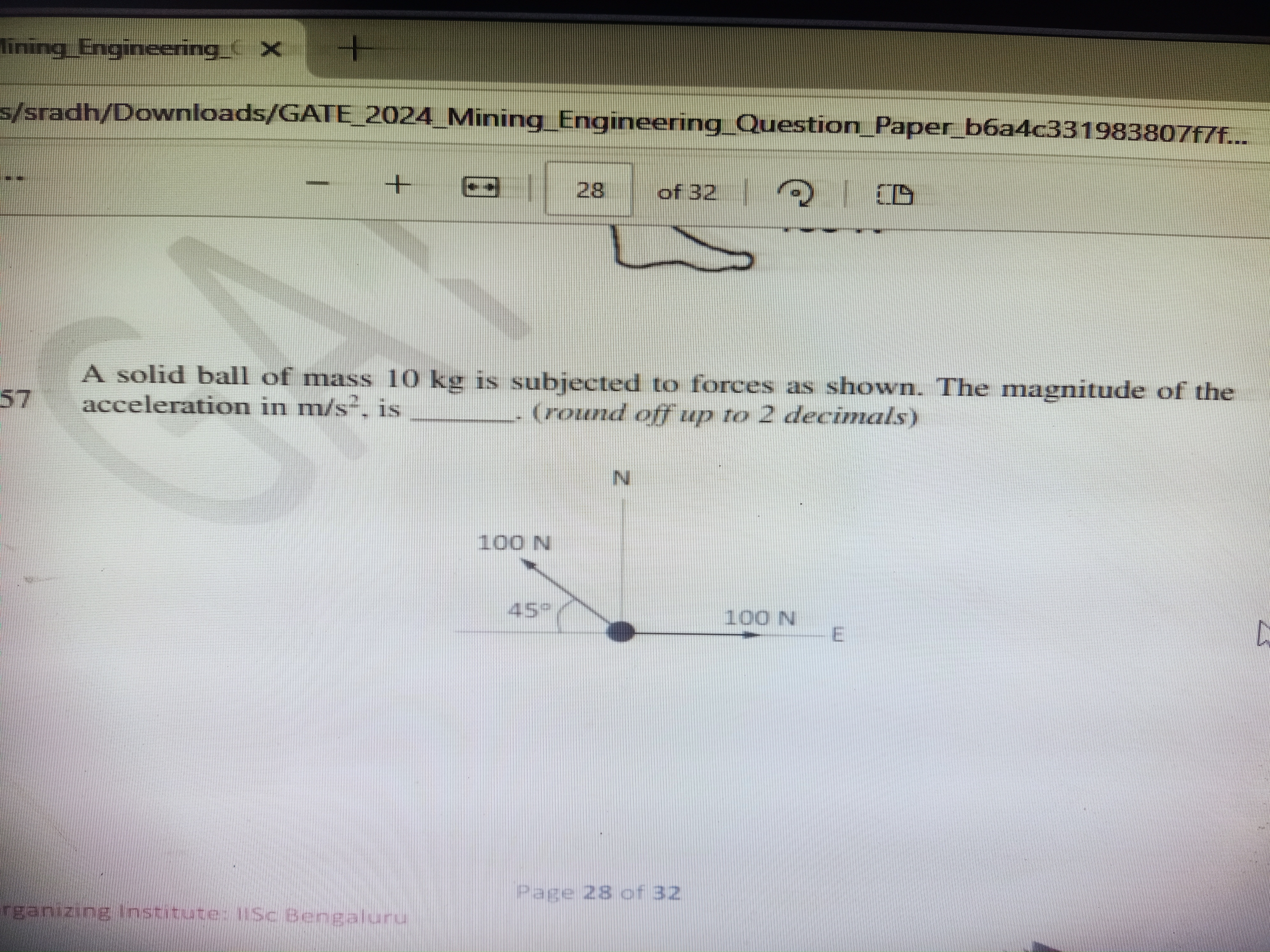
A solid ball of mass 10 kg is subjected to forces as shown. The magnitude of the acceleration in m/s² is ______. (round off up to 2 decimals)

Steps to Solve

1. Identify the forces acting on the ball

From the image, we see two forces acting on the ball:

• A force of 100 N directed to the east (horizontal).
• A force of 100 N directed at a 45° angle from the north (upwards).

2. Break down the forces into components

The force at a 45° angle can be broken down into its horizontal (x) and vertical (y) components.

For the 100 N force at 45°:

• The horizontal component, $F_{x1}$, is calculated as: $$ F_{x1} = 100 \cos(45°) = 100 \times \frac{\sqrt{2}}{2} = 70.71 , \text{N} $$

• The vertical component, $F_{y1}$, is calculated as: $$ F_{y1} = 100 \sin(45°) = 100 \times \frac{\sqrt{2}}{2} = 70.71 , \text{N} $$

3. Calculate the resultant forces in the x and y directions

Now, we can sum up the horizontal and vertical forces.

• The total horizontal force, $F_x$, is given by: $$ F_x = F_{x1} + 100 , \text{N} = 70.71 + 100 = 170.71 , \text{N} $$

• The total vertical force, $F_y$, is given by: $$ F_y = F_{y1} = 70.71 , \text{N} $$

4. Calculate the magnitude of the resultant force

The magnitude of the resultant force $F_R$ can be found using the Pythagorean theorem: $$ F_R = \sqrt{F_x^2 + F_y^2} $$ Substituting the values: $$ F_R = \sqrt{(170.71)^2 + (70.71)^2} $$

Calculating: $$ F_R = \sqrt{29142.99 + 5000.00} = \sqrt{34142.99} \approx 184.92 , \text{N} $$

5. Apply Newton's second law to find acceleration

Using Newton's second law, $F = ma$, where $m$ is the mass of the ball (10 kg), we find the acceleration $a$: $$ a = \frac{F_R}{m} = \frac{184.92}{10} = 18.49 , \text{m/s}^2 $$