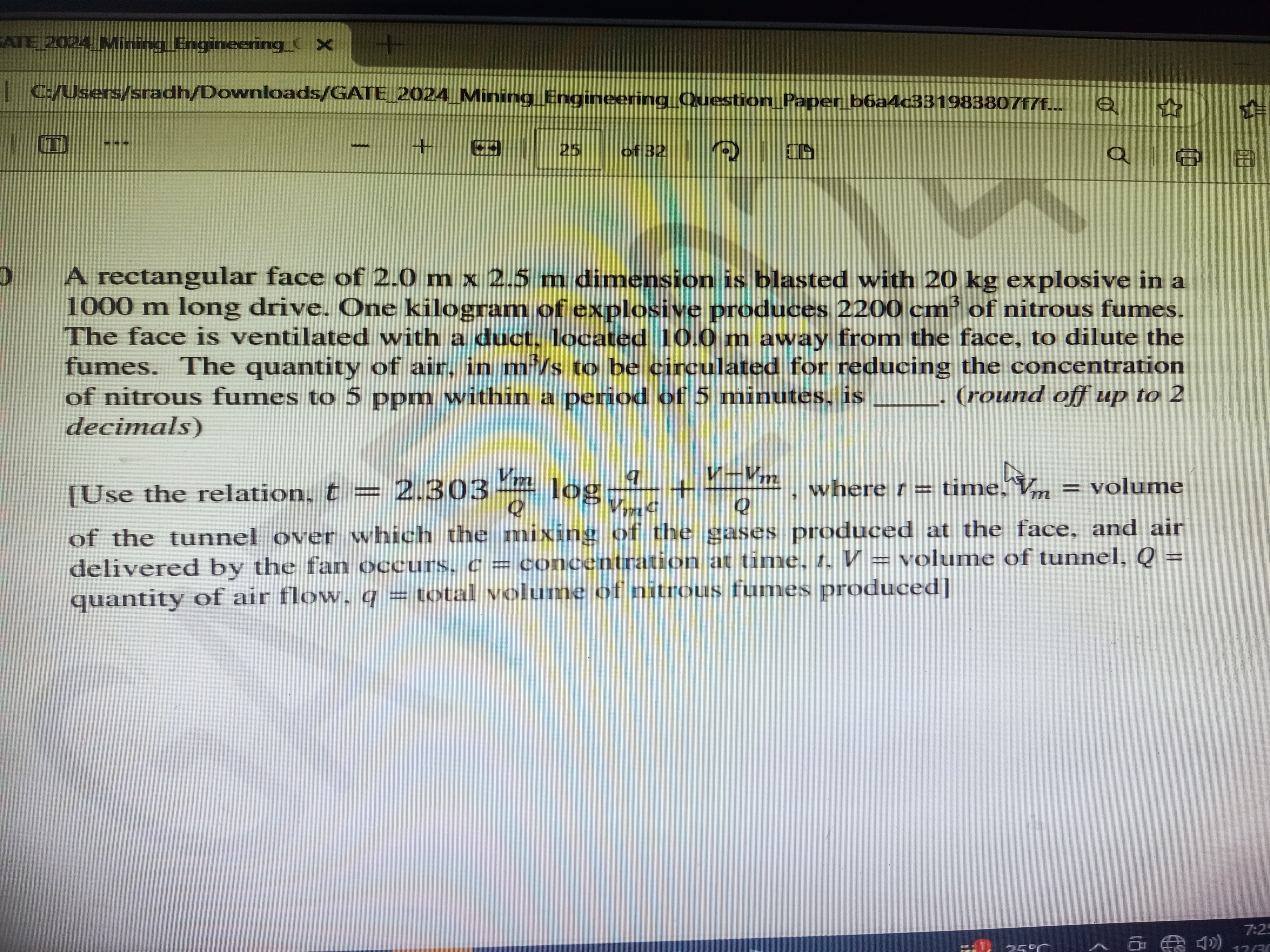
A rectangular face of 2.0 m x 2.5 m dimension is blasted with 20 kg explosive in a 1000 m long drive. One kilogram of explosive produces 2200 cm³ of nitrous fumes. The face is vent... A rectangular face of 2.0 m x 2.5 m dimension is blasted with 20 kg explosive in a 1000 m long drive. One kilogram of explosive produces 2200 cm³ of nitrous fumes. The face is ventilated with a duct, located 10.0 m away from the face, to dilute the fumes. The quantity of air, in m³/s to be circulated for reducing the concentration of nitrous fumes to 5 ppm within a period of 5 minutes, is _____ (round off up to 2 decimals).
Understand the Problem
The question involves calculating the quantity of air needed to dilute nitrous fumes in a mining scenario. It requires the use of a specific formula to determine the volume of air flow necessary to achieve a concentration of 5 ppm within a set time.
Answer
$Q \approx 4.50 \, \text{m}^3/\text{s}$
Answer for screen readers
The quantity of air required is approximately $Q \approx 4.50 , \text{m}^3/\text{s}$.
Steps to Solve
-
Calculate the total volume of nitrous fumes produced The problem states that 1 kg of explosive produces 2200 cm³ of nitrous fumes. Since there are 20 kg of explosives: [ q = 20 , \text{kg} \times 2200 , \text{cm}^3/\text{kg} = 44000 , \text{cm}^3 ] Convert this to m³: [ q = 44000 , \text{cm}^3 \times \frac{1 , \text{m}^3}{1000000 , \text{cm}^3} = 0.044 , \text{m}^3 ]
-
Determine the volume of the tunnel The tunnel dimensions are 2.0 m x 2.5 m x 1000 m. Thus, the volume (V) of the tunnel is: [ V = 2.0 , \text{m} \times 2.5 , \text{m} \times 1000 , \text{m} = 5000 , \text{m}^3 ]
-
Plug in the values into the equation The equation given is: [ t = 2.303 \times \frac{V_m}{Q} \log\left(\frac{g_c}{V_m}\right) + \frac{V - V_m}{Q} ] Where (g_c) is the concentration (5 ppm means 5/1,000,000 when converted). In this case, we will set (V_m) to the total volume of fumes produced (q):
- (V_m = 0.044 m^3)
- (t = 5 \times 60 = 300 , \text{s})
-
Rearrange the equation for (Q) To find (Q), we rearrange the equation: [ Q = \frac{2.303 \times V_m \log\left(\frac{g_c}{V_m}\right) + \frac{V - V_m}{t}}{t} ]
-
Calculate (Q) using numerical values Substitute the values and compute (Q): [ Q = \frac{2.303 \times 0.044 \log\left(\frac{5/1,000,000}{0.044}\right) + \frac{5000 - 0.044}{300}}{300} ]
-
Final Calculation for (Q) Calculate the logarithm and final value of (Q) to find the airflow required in m³/s.
The quantity of air required is approximately $Q \approx 4.50 , \text{m}^3/\text{s}$.
More Information
In mining operations, proper ventilation is crucial, especially when dealing with harmful gases like nitrous fumes. Achieving a dilution concentration of 5 ppm is an essential safety requirement in such environments.
Tips
- Forgetting to convert units (e.g., cm³ to m³) can lead to significant errors in calculations.
- Misunderstanding the significance of ppm and not correctly applying logarithmic calculations.
- Not properly substituting values into the formula.
AI-generated content may contain errors. Please verify critical information