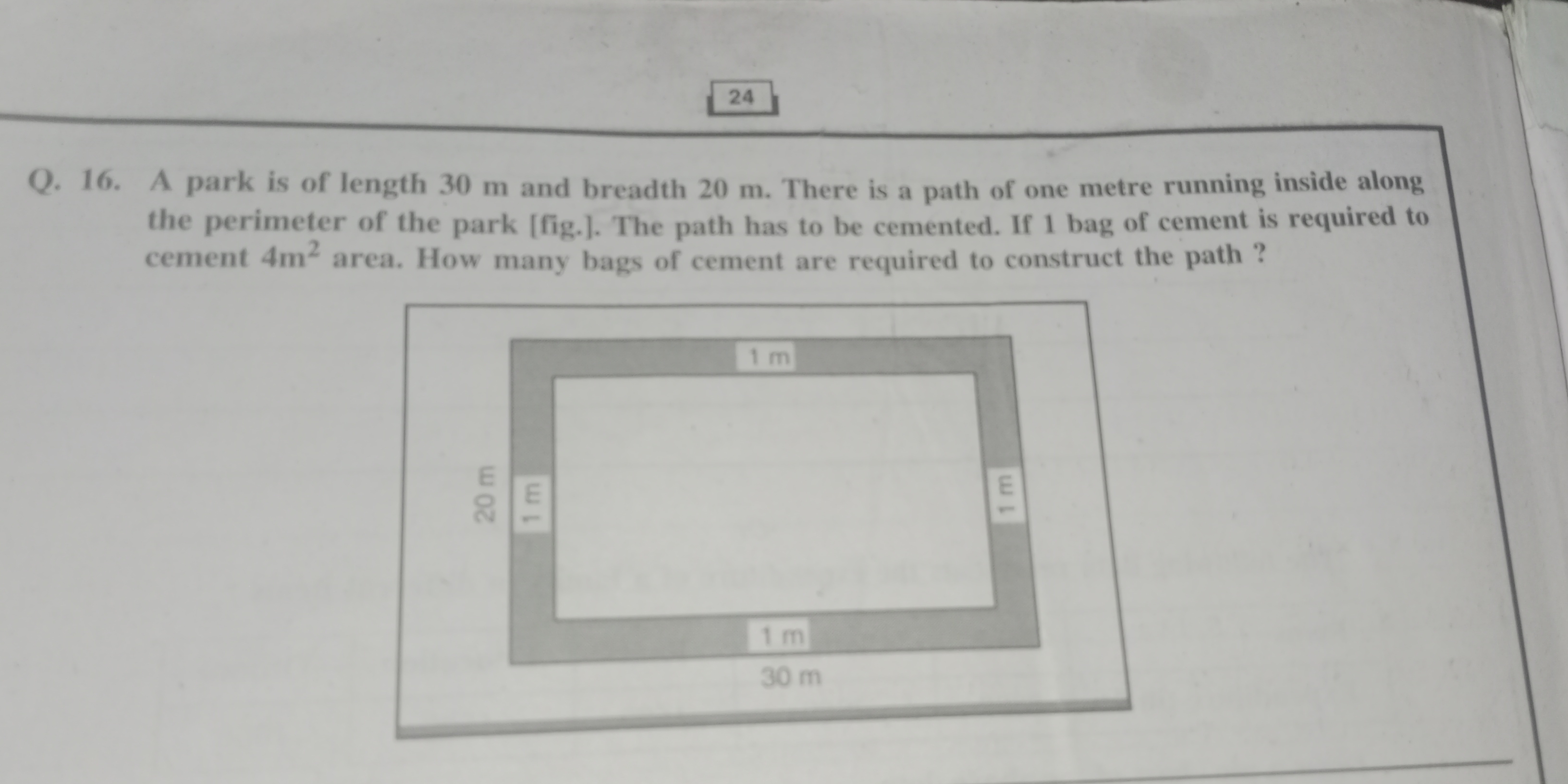
A park is of length 30 m and breadth 20 m. There is a path of one metre running inside along the perimeter of the park. The path has to be cemented. If 1 bag of cement is required... A park is of length 30 m and breadth 20 m. There is a path of one metre running inside along the perimeter of the park. The path has to be cemented. If 1 bag of cement is required to cement 4 sq m area. How many bags of cement are required to construct the path?
Understand the Problem
The question describes a rectangular park with a path running along the inside of its perimeter. We need to find the area of this path, and then determine how many bags of cement are needed to cover that area, given that one bag covers 4 square meters. The steps we need to do are to calculate the outside and inside areas, find the difference between those 2 areas and then divide this result by the cement coverage area to yield the number of cement bags.
Answer
24
Answer for screen readers
24 bags of cement are required to construct the path.
Steps to Solve
- Calculate the area of the park
The area of a rectangle is given by the formula: Area = length $\times$ breadth. The length of the park is 30 m and the breadth is 20 m. Therefore, the area of the park is: $30 \times 20 = 600 \ m^2$
- Determine the dimensions of the inner rectangle
Since the path is 1 meter wide and runs along the inside of the park, the length of the inner rectangle is reduced by 1 meter on each side (so a total of 2 meters), and the breadth is also reduced by 1 meter on each side (again, a total of 2 meters). Length of inner rectangle: $30 - 2(1) = 30 - 2 = 28 \ m$ Breadth of inner rectangle: $20 - 2(1) = 20 - 2 = 18 \ m$
- Calculate the area of the inner rectangle
Using the same area formula as before, the area of the inner rectangle is: $28 \times 18 = 504 \ m^2$
- Calculate the area of the path
The area of the path is the difference between the area of the park and the area of the inner rectangle: $600 - 504 = 96 \ m^2$
- Calculate the number of cement bags needed
Each bag of cement covers $4 \ m^2$. To find the number of bags needed, we divide the area of the path by the area covered by one bag: $96 \div 4 = 24$
24 bags of cement are required to construct the path.
More Information
This problem involves finding the area of a path within a rectangle by calculating the difference between the area of the outer rectangle and the area of the inner rectangle. Then, a simple division yields the number of bags required.
Tips
A common mistake is forgetting to subtract twice the path width from both the length and the width to determine the dimensions of the inner rectangle. Another mistake is miscalculating the area of either rectangle or making errors in the final division. Also forgetting the units.
AI-generated content may contain errors. Please verify critical information