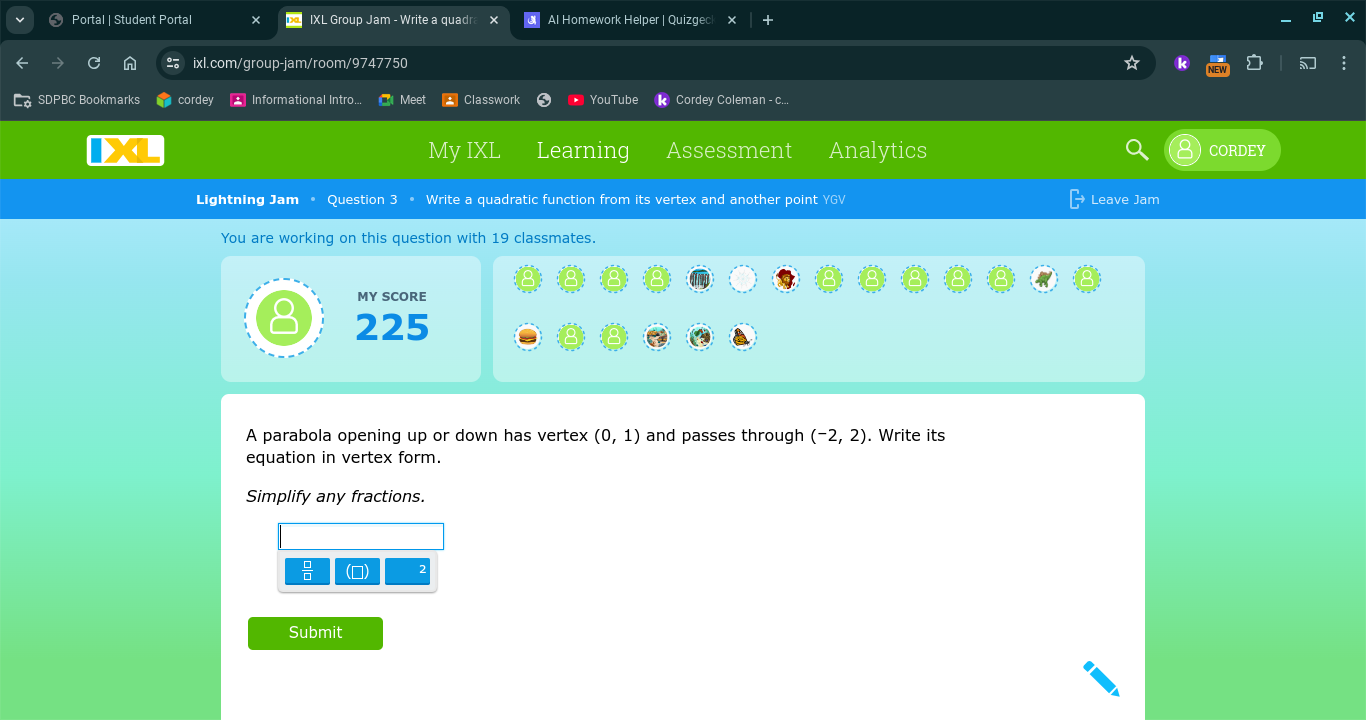
A parabola opening up or down has vertex (0, 1) and passes through (-2, 2). Write its equation in vertex form. Simplify any fractions.
Understand the Problem
The question is asking to write the equation of a parabola in vertex form given its vertex (0, 1) and a point that it passes through (-2, 2). This involves using the vertex form of a quadratic equation and substituting the known values to find the specific equation.
Answer
The equation of the parabola is $y = \frac{1}{4}x^2 + 1$.
Answer for screen readers
The equation of the parabola in vertex form is: $$ y = \frac{1}{4}x^2 + 1 $$
Steps to Solve
- Identify the vertex form of a parabola
The vertex form of a parabola is given by the equation: $$ y = a(x - h)^2 + k $$ where $(h, k)$ is the vertex of the parabola.
- Substitute the vertex values
Given that the vertex is at $(0, 1)$, we can substitute $h = 0$ and $k = 1$ into the vertex form: $$ y = a(x - 0)^2 + 1 $$ This simplifies to: $$ y = ax^2 + 1 $$
- Use the point to find the value of ( a )
We know the parabola passes through the point $(-2, 2)$. Substitute $x = -2$ and $y = 2$ into the equation: $$ 2 = a(-2)^2 + 1 $$ This simplifies to: $$ 2 = 4a + 1 $$
- Solve for ( a )
Subtract 1 from both sides to isolate $4a$: $$ 1 = 4a $$
Now divide by 4: $$ a = \frac{1}{4} $$
- Write the final equation
Substituting the value of ( a ) back into the equation gives: $$ y = \frac{1}{4}x^2 + 1 $$
The equation of the parabola in vertex form is: $$ y = \frac{1}{4}x^2 + 1 $$
More Information
This equation describes a parabola that opens upward with its vertex at (0, 1). The value of ( a = \frac{1}{4} ) indicates the width of the parabola; smaller values of ( a ) result in a wider parabola.
Tips
- Forgetting to substitute both values: Ensure that both vertex and point values are used in the calculations to find ( a ).
- Incorrectly simplifying algebraic steps: Double-check each algebraic manipulation, especially when isolating ( a ).
AI-generated content may contain errors. Please verify critical information