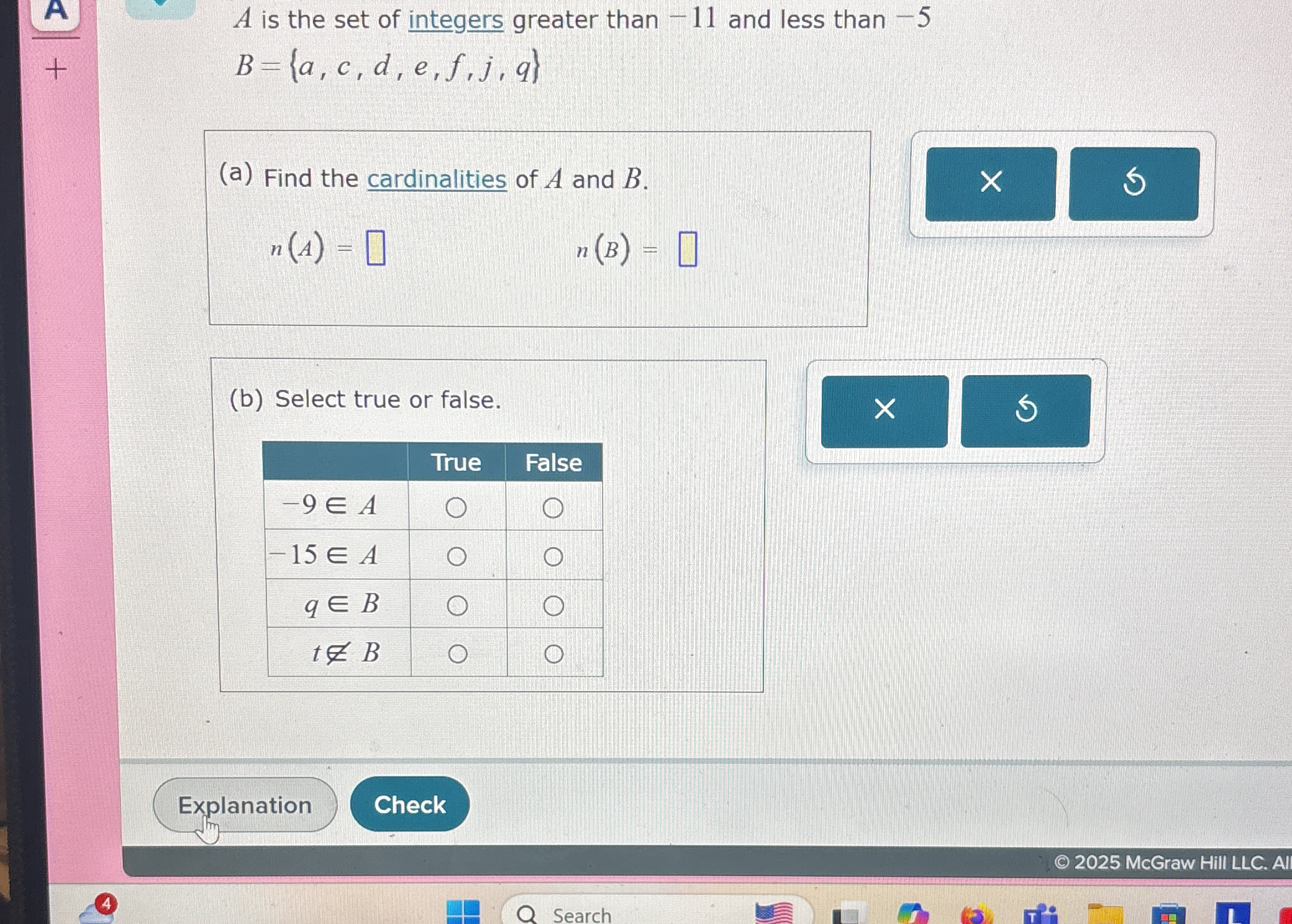
A is the set of integers greater than -11 and less than -5. B={a,c,d,e,f,j,q} (a) Find the cardinalities of A and B. n(A) = ? n(B) = ? (b) Select true or false. -9 ∈ A -15 ∈ A q... A is the set of integers greater than -11 and less than -5. B={a,c,d,e,f,j,q} (a) Find the cardinalities of A and B. n(A) = ? n(B) = ? (b) Select true or false. -9 ∈ A -15 ∈ A q ∈ B t ∉ B
Understand the Problem
The question involves set theory. Specifically,
- Part (a): It asks you to find the cardinality (number of elements) of set A, which consists of integers greater than -11 and less than -5, and set B, which is explicitly defined.
- Part (b): It presents a series of statements involving set membership and asks you to determine whether each statement is true or false.
Answer
$n(A) = 5$ $n(B) = 7$ -9 ∈ A: True -15 ∈ A: False q ∈ B: True t ∉ B: True
Answer for screen readers
$n(A) = 5$ $n(B) = 7$
-9 ∈ A: True -15 ∈ A: False q ∈ B: True t ∉ B: True
Steps to Solve
- Find the elements of set A
Set A contains integers greater than -11 and less than -5. So, $A = {-10, -9, -8, -7, -6}$.
- Determine the cardinality of set A
The cardinality of a set is the number of elements in the set. $A = {-10, -9, -8, -7, -6}$ has 5 elements. Therefore, $n(A) = 5$.
- Determine the cardinality of set B
Set B is given as $B = {a, c, d, e, f, j, q}$. Count the number of elements in B. There are 7 elements in B. Therefore, $n(B) = 7$.
- Evaluate the statement -9 ∈ A
The statement $-9 \in A$ means "-9 is an element of set A". From step 1, we know that $A = {-10, -9, -8, -7, -6}$. Since -9 is in the set A, the statement is True.
- Evaluate the statement -15 ∈ A
The statement $-15 \in A$ means "-15 is an element of set A". From step 1, we know that $A = {-10, -9, -8, -7, -6}$. Since -15 is not in the set A, the statement is False.
- Evaluate the statement q ∈ B
The statement $q \in B$ means "q is an element of set B". We are given $B = {a, c, d, e, f, j, q}$. Since q is in the set B, the statement is True.
- Evaluate the statement t ∉ B
The statement $t \notin B$ means "t is not an element of set B". We are given $B = {a, c, d, e, f, j, q}$. Since t is not in set B, the statement is True.
$n(A) = 5$ $n(B) = 7$
-9 ∈ A: True -15 ∈ A: False q ∈ B: True t ∉ B: True
More Information
Cardinality refers to the number of elements within a set. The symbol "∈" denotes set membership, while "∉" indicates that an element is not a member of a particular set.
Tips
A common mistake is miscounting the elements in the sets and calculating the cardinality incorrectly. Another common mistake is misunderstanding the set membership notation (∈ and ∉) and incorrectly determining if an element belongs to a set or not.
AI-generated content may contain errors. Please verify critical information