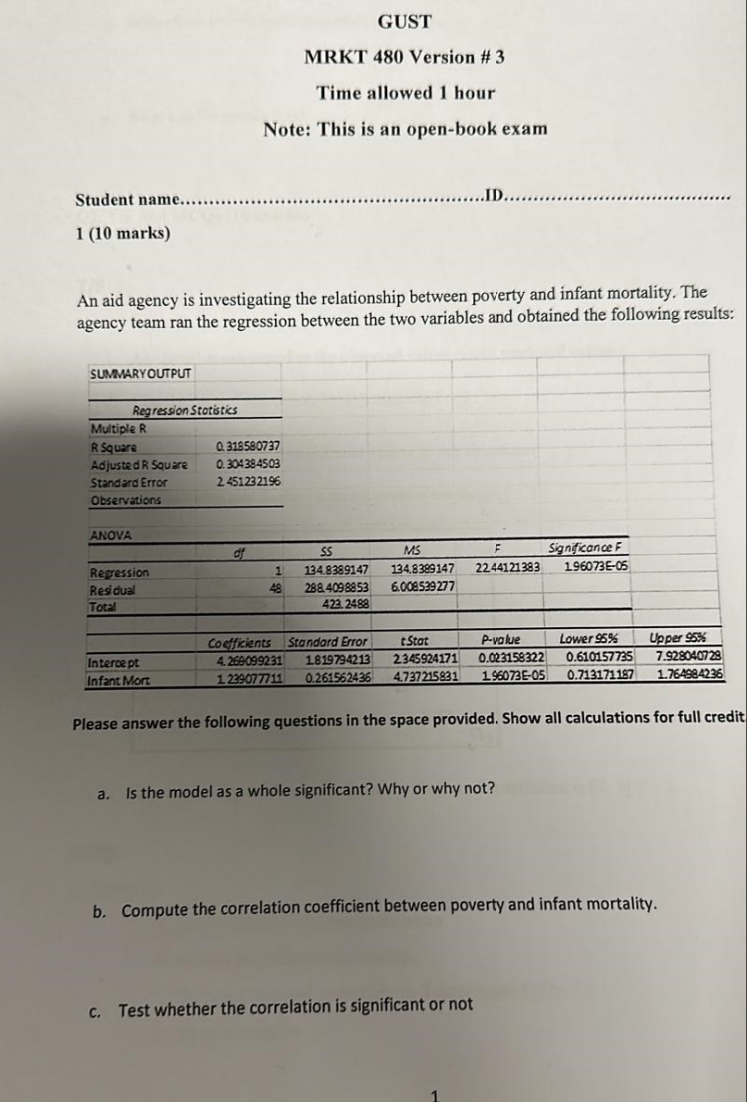
a. Is the model as a whole significant? Why or why not? b. Compute the correlation coefficient between poverty and infant mortality. c. Test whether the correlation is significant... a. Is the model as a whole significant? Why or why not? b. Compute the correlation coefficient between poverty and infant mortality. c. Test whether the correlation is significant or not.
Understand the Problem
The question requires an analysis of regression statistics to determine the significance of the model, compute the correlation coefficient, and test its significance. It focuses on the relationship between poverty and infant mortality using statistical output.
Answer
a. Yes, significant; b. $R = 0.318580737$; c. Yes, significant.
Answer for screen readers
a. Yes, the model is significant because the p-value ($1.96073 \times 10^{-5}$) is less than $0.05$.
b. The correlation coefficient between poverty and infant mortality is $R = 0.318580737$.
c. Yes, the correlation is significant since the p-value ($1.96073 \times 10^{-5}$) is less than $0.05$.
Steps to Solve
-
Check Overall Model Significance
To determine if the model is significant, we look at the p-value from the ANOVA table. The reported p-value is $1.96073 \times 10^{-5}$.
We compare the p-value to a significance level (commonly $\alpha = 0.05$).
If $p < 0.05$, the model is significant.
-
Compute Correlation Coefficient
The correlation coefficient (Multiple R) is provided in the regression statistics.
From the output, we have:
$$ R = 0.318580737 $$
This value indicates the strength and direction of the linear relationship between the two variables.
-
Test Correlation Significance
To check if the correlation is significant, we can use the t-statistic and its corresponding p-value for the correlation.
The relevant t-statistic for "Infant Mort" is $4.737215831$ with a corresponding p-value of $1.96073 \times 10^{-5}$.
Again, we compare the p-value to our significance level.
If the p-value ($1.96073 \times 10^{-5}$) is less than $0.05$, we conclude the correlation is significant.
a. Yes, the model is significant because the p-value ($1.96073 \times 10^{-5}$) is less than $0.05$.
b. The correlation coefficient between poverty and infant mortality is $R = 0.318580737$.
c. Yes, the correlation is significant since the p-value ($1.96073 \times 10^{-5}$) is less than $0.05$.
More Information
The low p-value indicates strong evidence against the null hypothesis, suggesting that poverty is significantly related to infant mortality. The correlation coefficient shows a moderate positive relationship between the two variables.
Tips
- Confusing the p-value with the significance level. Always ensure you compare the correct values.
- Misinterpreting the correlation coefficient. Remember, a higher value indicates a stronger positive relationship, while a lower value indicates weaker or no relationship.
AI-generated content may contain errors. Please verify critical information