A curve has equation y = x^3 - 6x^2 + 16. Find the coordinates of the two turning points.
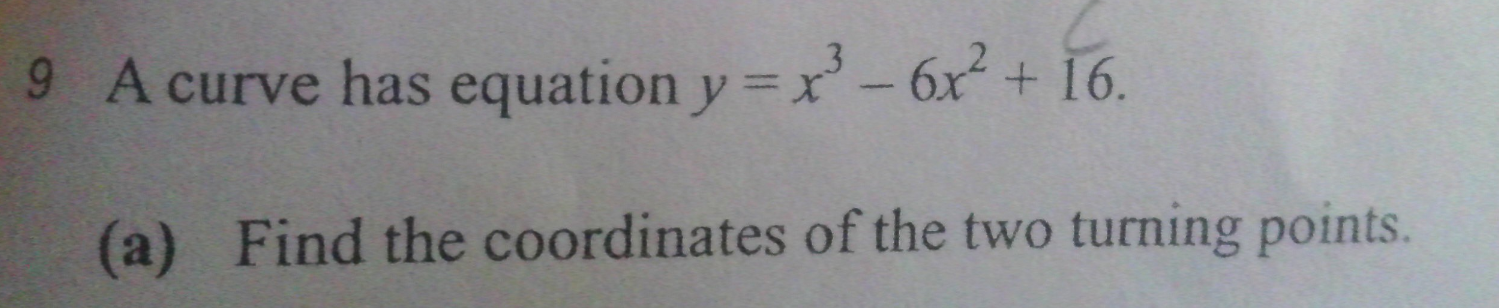
Understand the Problem
The question asks to find the coordinates of the two turning points of the curve given by the equation y = x^3 - 6x^2 + 16. This involves finding the first derivative of the equation, setting it to zero to find the x-coordinates of the turning points, and then substituting those x-values back into the original equation to find the corresponding y-coordinates.
Answer
$(0, 16)$ and $(4, -16)$
Answer for screen readers
The coordinates of the two turning points are $(0, 16)$ and $(4, -16)$.
Steps to Solve
- Find the first derivative
To find the turning points, we need to find where the slope of the curve is zero. This means we need to find the first derivative of the function $y = x^3 - 6x^2 + 16$ and set it equal to zero. The power rule states that the derivative of $x^n$ is $nx^{n-1}$. Applying this to each term gives:
$$ \frac{dy}{dx} = 3x^2 - 12x $$
- Set the derivative equal to zero and solve for x
Now we set the derivative equal to zero and solve for $x$:
$$ 3x^2 - 12x = 0 $$ We can factor out a $3x$ from the equation:
$$ 3x(x - 4) = 0 $$ This gives us two possible solutions for $x$: $$ 3x = 0 \Rightarrow x = 0 $$ $$ x - 4 = 0 \Rightarrow x = 4 $$
- Find the corresponding y-coordinates
Substitute the $x$-values we found ($x = 0$ and $x = 4$) back into the original equation $y = x^3 - 6x^2 + 16$ to find the corresponding $y$-coordinates.
For $x = 0$: $$ y = (0)^3 - 6(0)^2 + 16 = 0 - 0 + 16 = 16 $$ So, one turning point is at $(0, 16)$.
For $x = 4$: $$ y = (4)^3 - 6(4)^2 + 16 = 64 - 6(16) + 16 = 64 - 96 + 16 = -16 $$ So, the other turning point is at $(4, -16)$.
- State the coordinates of the turning points
Therefore, the coordinates of the two turning points are $(0, 16)$ and $(4, -16)$.
The coordinates of the two turning points are $(0, 16)$ and $(4, -16)$.
More Information
Turning points are sometimes referred to as stationary points, because the gradient of the curve is momentarily zero there. They can be local maxima, local minima, or saddle points (points of inflection).
Tips
A common mistake is forgetting to substitute the $x$-values back into the original equation to find the $y$-coordinates. Another mistake is to make errors when differentiating the original equation. Finally, errors in the algebraic manipulation when solving the quadratic equation obtained by setting the first derivative to zero are very common.
AI-generated content may contain errors. Please verify critical information