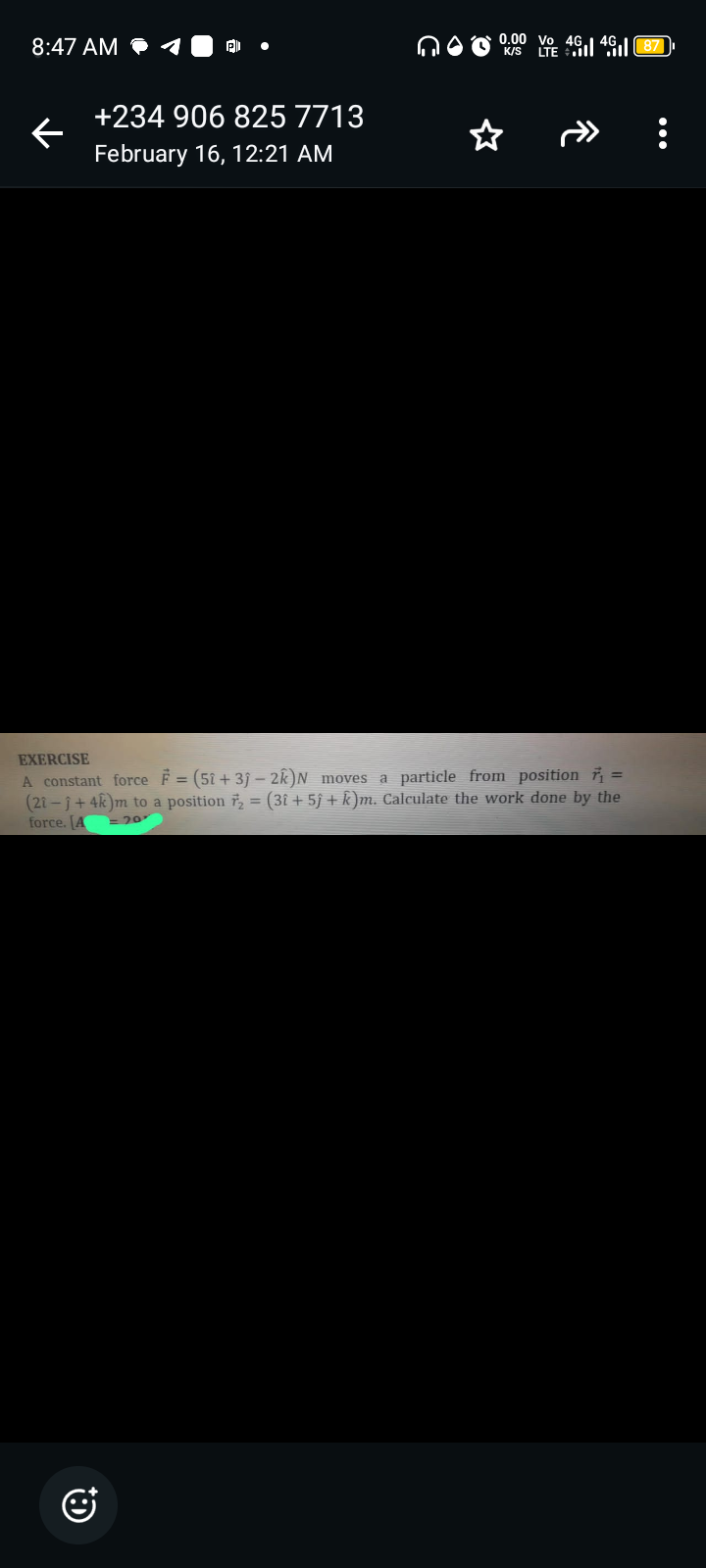
A constant force \(\vec{F} = (5\hat{i} + 3\hat{j} - 2\hat{k})\) N moves a particle from position \(\vec{r_1} = (2\hat{i} - \hat{j} + 4\hat{k})\) m to a position \(\vec{r_2} = (3\ha... A constant force \(\vec{F} = (5\hat{i} + 3\hat{j} - 2\hat{k})\) N moves a particle from position \(\vec{r_1} = (2\hat{i} - \hat{j} + 4\hat{k})\) m to a position \(\vec{r_2} = (3\hat{i} + 5\hat{j} + \hat{k})\) m. Calculate the work done by the force.
Understand the Problem
The question asks to calculate the work done by a constant force on a particle as it moves from one position to another. We will use the formula W = F . d, where W is work done, F is the force vector, and d is the displacement vector. We calculate d by subtracting the initial position vector r1 from the final position vector r2, d = r2 - r1.
Answer
$29$ J
Answer for screen readers
The work done by the force is $29$ J.
Steps to Solve
- Calculate the displacement vector $\vec{d}$
The displacement vector $\vec{d}$ is the difference between the final position vector $\vec{r_2}$ and the initial position vector $\vec{r_1}$. $$ \vec{d} = \vec{r_2} - \vec{r_1} $$ $$ \vec{d} = (3\hat{i} + 5\hat{j} + \hat{k}) - (2\hat{i} - \hat{j} + 4\hat{k}) $$ $$ \vec{d} = (3-2)\hat{i} + (5-(-1))\hat{j} + (1-4)\hat{k} $$ $$ \vec{d} = (1\hat{i} + 6\hat{j} - 3\hat{k}) \text{ m} $$
- Calculate the work done $W$
The work done $W$ is the dot product of the force vector $\vec{F}$ and the displacement vector $\vec{d}$. $$ W = \vec{F} \cdot \vec{d} $$ $$ W = (5\hat{i} + 3\hat{j} - 2\hat{k}) \cdot (\hat{i} + 6\hat{j} - 3\hat{k}) $$ $$ W = (5 \times 1) + (3 \times 6) + (-2 \times -3) $$ $$ W = 5 + 18 + 6 $$ $$ W = 29 \text{ J} $$
The work done by the force is $29$ J.
More Information
The work done is a scalar quantity that represents the energy transferred to or from an object by a force acting on it. In this case, the work done by the constant force on the particle is 29 Joules, indicating that 29 Joules of energy has been transferred to the particle.
Tips
A common mistake is to subtract the final position vector from the initial position vector, resulting in a displacement vector with reversed signs. This leads to an incorrect calculation of the work done. Also, errors can occur during the dot product calculation if the components are not correctly multiplied and added, especially with negative signs.
AI-generated content may contain errors. Please verify critical information