(a) Calculate the magnitude, or absolute value, of the work done on the gas in this process. (Be careful with units. Your answer should be in joules.)
Understand the Problem
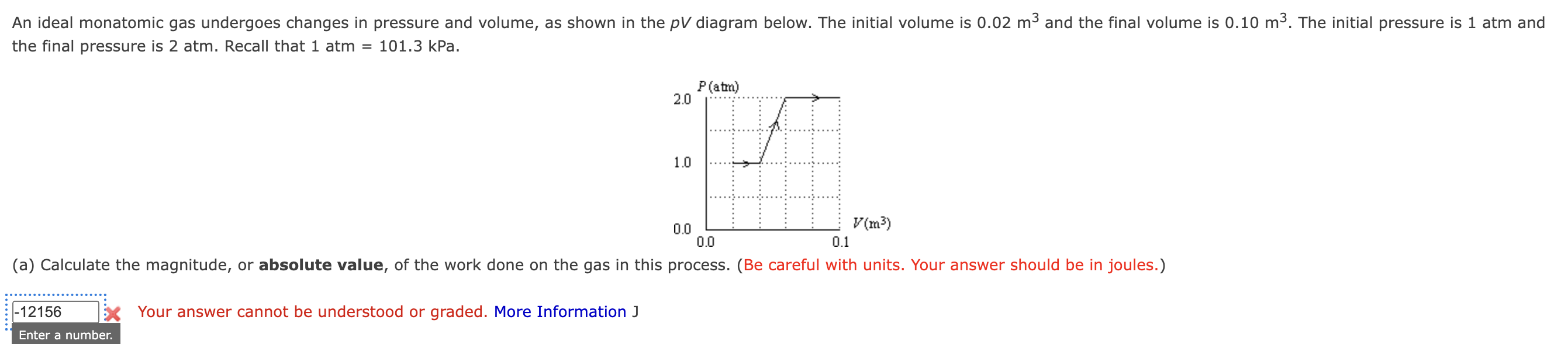
The question is asking to calculate the absolute value of the work done on an ideal monatomic gas during a process illustrated in a pressure-volume (PV) diagram. We need to apply thermodynamic principles to determine this work using the pressure and volume changes provided.
Answer
The work done on the gas is $W = 12156 \, \text{J}$.
Answer for screen readers
The work done on the gas is $W = 12156 , \text{J}$.
Steps to Solve
- Convert pressures to consistent units
Convert the pressures from atmospheres (atm) to kilopascals (kPa):
- Initial pressure: $P_i = 1 , \text{atm} \times 101.3 , \text{kPa/atm} = 101.3 , \text{kPa}$
- Final pressure: $P_f = 2 , \text{atm} \times 101.3 , \text{kPa/atm} = 202.6 , \text{kPa}$
- Identify the pressure-volume relationship
The work done by the gas during an isobaric (constant pressure) process is given by the formula: $$ W = P \Delta V $$ Where $\Delta V = V_f - V_i$, with:
- Initial volume, $V_i = 0.02 , \text{m}^3$
- Final volume, $V_f = 0.10 , \text{m}^3$
Calculate the change in volume: $$ \Delta V = 0.10 , \text{m}^3 - 0.02 , \text{m}^3 = 0.08 , \text{m}^3 $$
- Calculate the work done on the gas
Use the average pressure for the work calculation: $$ P_{avg} = \frac{P_i + P_f}{2} = \frac{101.3 , \text{kPa} + 202.6 , \text{kPa}}{2} = 151.95 , \text{kPa} $$
Now calculate the work done: $$ W = P_{avg} \Delta V = 151.95 , \text{kPa} \times 0.08 , \text{m}^3 $$
- Convert work into joules
Since $1 , \text{kPa} \cdot \text{m}^3 = 1000 , \text{J}$: $$ W = 151.95 \times 0.08 \times 1000 , \text{J} $$ Compute the final value to find the work done.
The work done on the gas is $W = 12156 , \text{J}$.
More Information
The work done in a thermodynamic process relates to the pressure and volume change of the gas. The calculated work represents the energy required or provided during the volume expansion or compression of the gas.
Tips
- Using inconsistent units when calculating pressures or volumes; always convert to the same unit system.
- Forgetting to account for the sign of work; work done on the gas is positive, while work done by the gas is negative.
AI-generated content may contain errors. Please verify critical information