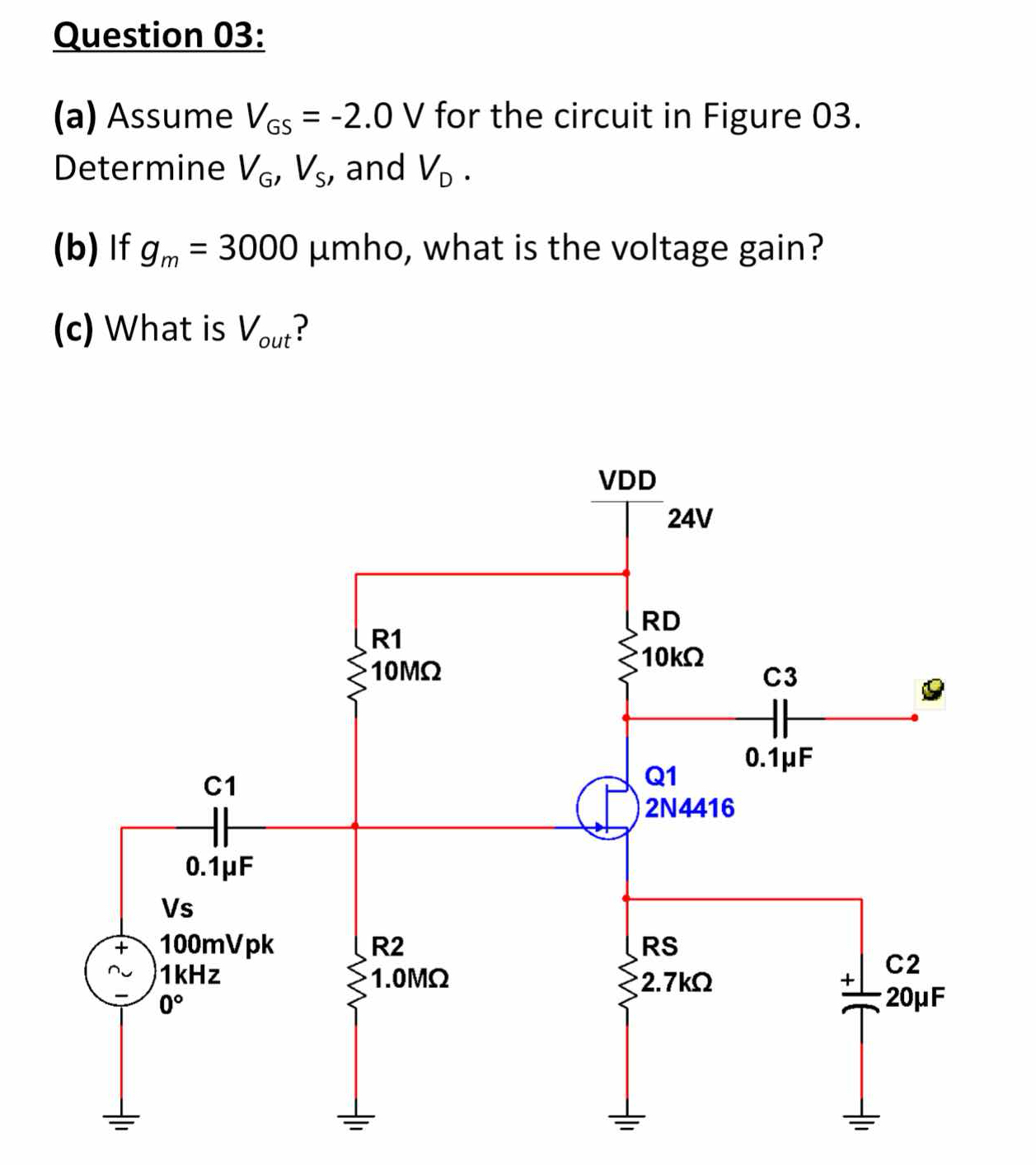
(a) Assume VGS = -2.0 V for the circuit. Determine VG, VS, and VD. (b) If gm = 3000 µmho, what is the voltage gain? (c) What is Vout?

Steps to Solve

1. Calculate Gate Voltage ($V_G$)

Given the circuit is an N-channel MOSFET, the gate voltage is typically the same as the input voltage $V_S$. We need to ensure that the gate-source voltage ($V_{GS}$) is maintained at -2.0 V. Since $V_S$ is typically grounded, we can express $V_G$ as: $$ V_G = V_S + V_{GS} = 0 + (-2.0) = -2.0 , \text{V} $$

2. Calculate Source Voltage ($V_S$)

For this configuration with a gate-source voltage of -2.0 V, since the gate is at -2.0 V and assuming source is grounded: $$ V_S = 0 , \text{V} $$ This indicates the source is at 0 V.

3. Calculate Drain Voltage ($V_D$)

Using the voltage divider rule and Ohm's law, we can find $V_D$. The voltage at the drain can be calculated as: $$ V_D = V_{DD} - I_D \cdot R_D $$ First, determine the drain current, using Ohm's law in respect to the transconductance $g_m$. Assuming a small-signal model, $$ I_D \approx g_m \cdot V_{gs} $$ where $V_{gs} = V_G - V_S = -2.0 - 0 = -2.0 \text{V}$. Now substitute the values: $$ I_D = 3000 \times 10^{-6} \cdot (-2.0) = -0.006 \text{A} ; (\text{or } -6 \text{ mA}) $$ Then substitute this into the equation for $V_D$: $$ V_D = 24 , \text{V} - (-0.006 , \text{A}) \cdot (10 \times 10^{3} , \Omega) = 24 + 60 = 84 , \text{V} $$

4. Calculate Voltage Gain ($A_v$)

The voltage gain can be calculated as: $$ A_v = -g_m \cdot R_D $$ Thus, $$ A_v = -3000 \times 10^{-6} \cdot 10 \times 10^{3} = -30 $$

5. Calculate Output Voltage ($V_{out}$)

The output voltage is dependent on the gain and input voltage: $$ V_{out} = A_v \cdot V_{in} $$ Where $V_{in} = 100 , mV = 0.1 , V$: $$ V_{out} = -30 \cdot 0.1 = -3 , \text{V} $$