A + A' = I के लिए α का मान क्या है?
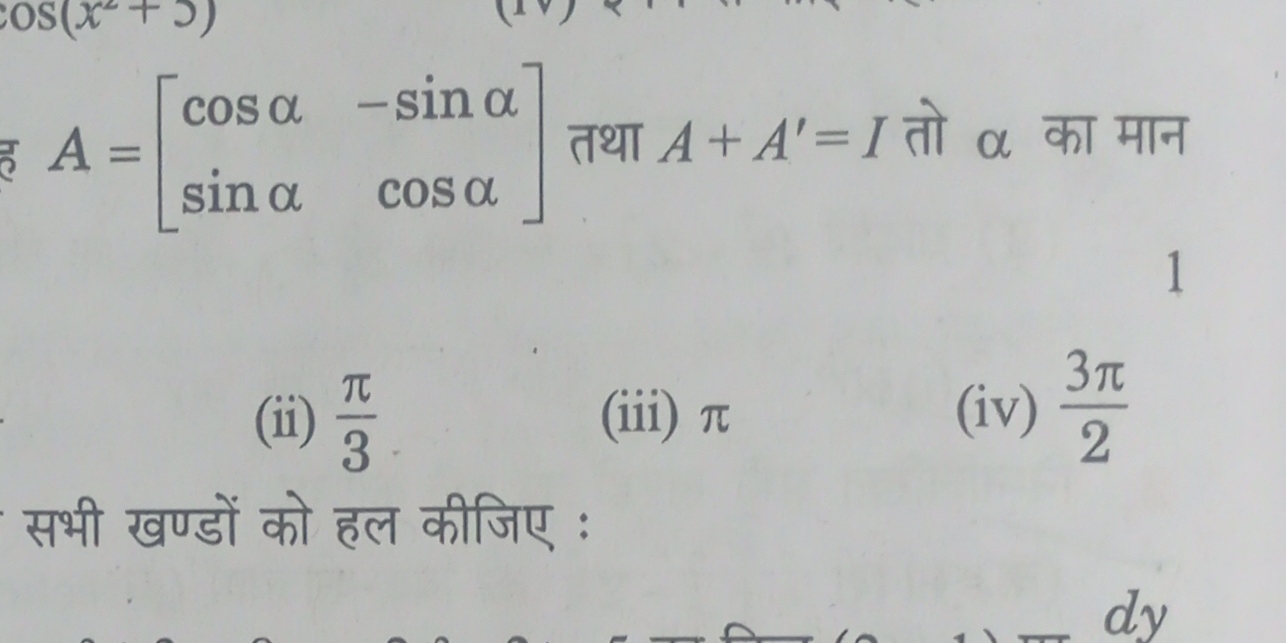
Understand the Problem
प्रश्न में एक मैट्रिक्स A दिया गया है और यह पता करने के लिए कहा गया है कि A + A' = I होने पर α का मान क्या होगा। यहाँ 'I' एक पहचान मैट्रिक्स है।
Answer
The value of \( \alpha \) is \( \frac{\pi}{3} \).
Answer for screen readers
The value of ( \alpha ) is ( \frac{\pi}{3} ).
Steps to Solve
-
Understanding the Matrix A and its Transpose Given matrix ( A ) is defined as: $$ A = \begin{bmatrix} \cos \alpha & -\sin \alpha \ \sin \alpha & \cos \alpha \end{bmatrix} $$ The transpose of matrix ( A ), denoted as ( A' ), is: $$ A' = \begin{bmatrix} \cos \alpha & \sin \alpha \ -\sin \alpha & \cos \alpha \end{bmatrix} $$
-
Calculating A + A' Now we will add ( A ) and ( A' ): $$ A + A' = \begin{bmatrix} \cos \alpha & -\sin \alpha \ \sin \alpha & \cos \alpha \end{bmatrix} + \begin{bmatrix} \cos \alpha & \sin \alpha \ -\sin \alpha & \cos \alpha \end{bmatrix} $$ Performing the addition results in: $$ A + A' = \begin{bmatrix} 2\cos \alpha & 0 \ 0 & 2\cos \alpha \end{bmatrix} = 2\cos \alpha \begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix} $$
-
Setting A + A' Equal to the Identity Matrix According to the problem, we need: $$ A + A' = I $$ where ( I ) is the identity matrix: $$ I = \begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix} $$ Thus, we equate: $$ 2\cos \alpha = 1 $$
-
Solving for α From the equation ( 2\cos \alpha = 1 ), we isolate ( \cos \alpha ): $$ \cos \alpha = \frac{1}{2} $$ The general solutions for ( \alpha ) are: $$ \alpha = \frac{\pi}{3} + 2k\pi \quad \text{or} \quad \alpha = -\frac{\pi}{3} + 2k\pi, \quad k \in \mathbb{Z} $$
The value of ( \alpha ) is ( \frac{\pi}{3} ).
More Information
The cosine of ( \frac{\pi}{3} ) is ( \frac{1}{2} ), which satisfies the equation ( 2\cos \alpha = 1 ). This indicates specific angles in the unit circle where the cosine function takes this value.
Tips
Common mistakes include:
- Forgetting to account for the periodic nature of trigonometric functions, which can lead to missing other valid solutions.
- Incorrectly adding matrices, particularly when summing off-diagonal elements.
AI-generated content may contain errors. Please verify critical information