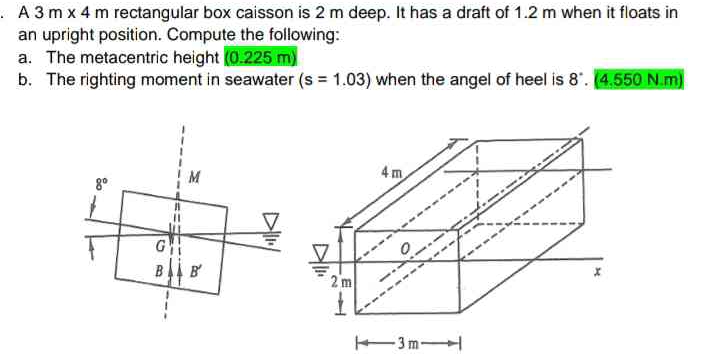
A 3m x 4m rectangular box caisson is 2m deep. It has a draft of 1.2m when it floats in an upright position. Compute the following: a. The metacentric height b. The righting moment... A 3m x 4m rectangular box caisson is 2m deep. It has a draft of 1.2m when it floats in an upright position. Compute the following: a. The metacentric height b. The righting moment in seawater (s=1.03) when the angle of heel is 8 degrees.
Understand the Problem
The question describes a rectangular box caisson and asks us to calculate the metacentric height and the righting moment in seawater given the dimensions of the caisson, its draft, and the angle of heel. This appears to be a homework question related to naval architecture or fluid mechanics.
Answer
a. $GM = 0.711 \text{ m}$ b. $RM = 14546.86 \text{ N} \cdot \text{m}$
Answer for screen readers
a. The metacentric height is $0.711 \text{ m}$ b. The righting moment is $14546.86 \text{ N} \cdot \text{m}$
Steps to Solve
- Calculate the vertical distance from the keel to the center of buoyancy (KB)
Since the caisson is rectangular, the center of buoyancy is simply half of the draft. $KB = \frac{draft}{2} = \frac{1.2 \text{ m}}{2} = 0.6 \text{ m}$
-
Calculate the vertical distance from the keel to the center of gravity (KG) Since the caisson is a uniform rectangular box, the center of gravity is half of the total depth. $KG = \frac{depth}{2} = \frac{2 \text{ m}}{2} = 1.0 \text{ m}$
-
Calculate the second moment of area (I) $I = \frac{L B^3}{12} = \frac{3 \text{ m} \cdot (4 \text{ m})^3}{12}= \frac{3 \text{ m} \cdot 64 \text{ m}^3}{12} = 16 \text{ m}^4$
-
Calculate the displaced volume ($V$) $V = L \cdot B \cdot draft = 3 \text{ m} \cdot 4 \text{ m} \cdot 1.2 \text{ m} = 14.4 \text{ m}^3$
-
Calculate the distance between the center of buoyancy and the metacenter (BM) $BM = \frac{I}{V} = \frac{16 \text{ m}^4}{14.4 \text{ m}^3} = 1.111 \text{ m}$
-
Calculate the metacentric height (GM) $GM = BM - KG + KB = 1.111 \text{ m} + 0.6 \text{ m} - 1.0 \text{ m} = 0.711 \text{ m}$
-
Calculate the density of seawater ($\rho$) $ \rho = s \cdot \rho_{freshwater} = 1.03 \cdot 1000 \frac{\text{kg}}{\text{m}^3} = 1030 \frac{\text{kg}}{\text{m}^3} $
-
Calculate the weight density of seawater ($\gamma$) $ \gamma = \rho \cdot g = 1030 \frac{\text{kg}}{\text{m}^3} \cdot 9.81 \frac{\text{m}}{\text{s}^2} = 10104.3 \frac{\text{N}}{\text{m}^3}$
-
Calculate the righting moment (RM) $RM = \gamma \cdot V \cdot GM \cdot \sin{\theta} = 10104.3 \frac{\text{N}}{\text{m}^3} \cdot 14.4 \text{ m}^3 \cdot 0.711 \text{ m} \cdot \sin{8^\circ} = 10104.3 \frac{\text{N}}{\text{m}^3} \cdot 14.4 \text{ m}^3 \cdot 0.711 \text{ m} \cdot 0.139 = 14546.86 \text{ N} \cdot \text{m}$
a. The metacentric height is $0.711 \text{ m}$ b. The righting moment is $14546.86 \text{ N} \cdot \text{m}$
More Information
The metacentric height is a measure of a vessel's initial stability. A larger metacentric height indicates greater initial stability and resistance to overturning. The righting moment is the moment that restores a vessel to an upright position after it has been heeled over.
Tips
A common mistake is to confuse KB and KG -- many students will think these two values are equivalent. Another common mistake is using the wrong units or forgetting to convert units when calculating the righting moment. A third common mistake is accidentally using the cosine function instead of the sine function (or vice versa) when computing the righting arm.
AI-generated content may contain errors. Please verify critical information