9.4√3 + 2√12
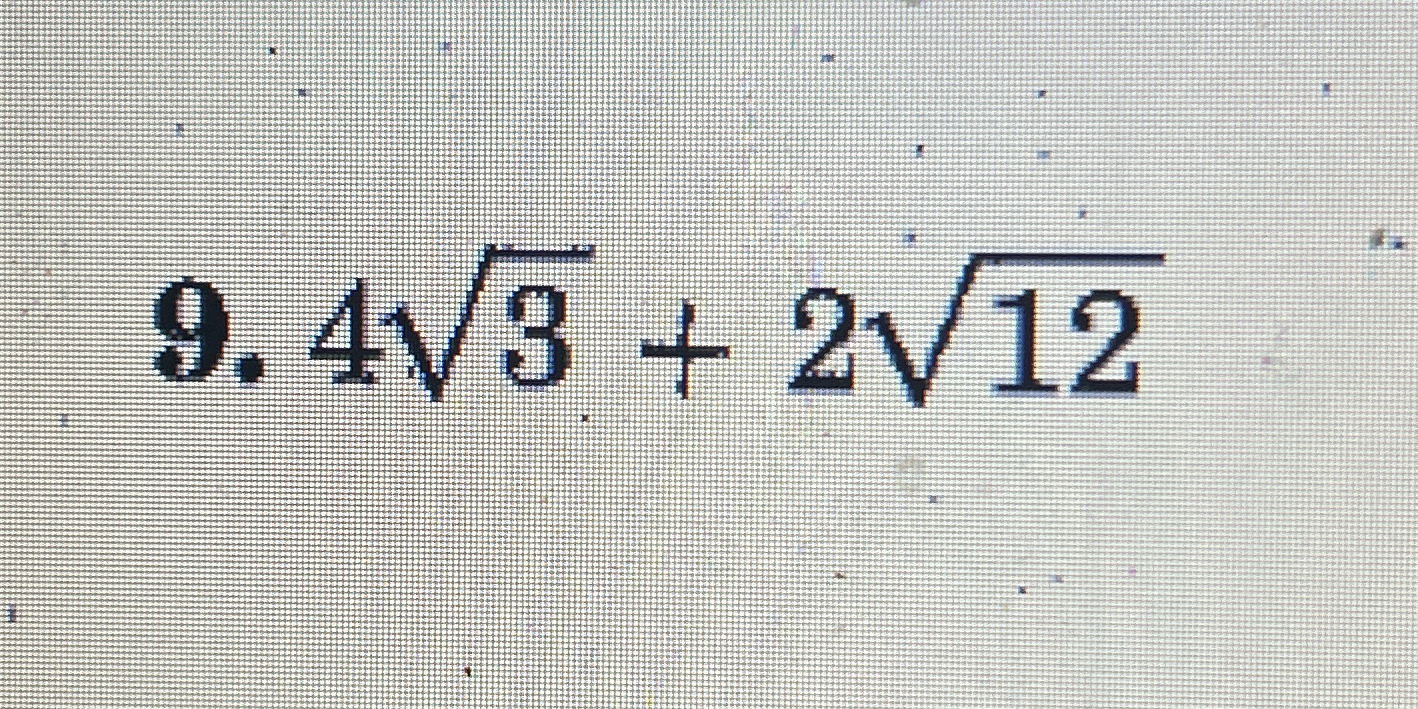
Understand the Problem
The question involves simplifying the expression that includes square roots. It asks us to combine the terms 9.4√3 and 2√12, where √12 can be simplified to 2√3, allowing us to combine the like terms.
Answer
$13.4\sqrt{3}$
Answer for screen readers
The simplified expression is $13.4\sqrt{3}$.
Steps to Solve
-
Simplify the square root
The expression contains $2\sqrt{12}$. We can simplify $\sqrt{12}$ as follows:
$$ \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3} $$
Therefore,
$$ 2\sqrt{12} = 2 \cdot 2\sqrt{3} = 4\sqrt{3} $$
-
Combine like terms
Now that we have simplified $2\sqrt{12}$ to $4\sqrt{3}$, we can combine it with $9.4\sqrt{3}$.
We have:
$$ 9.4\sqrt{3} + 4\sqrt{3} $$
Since both terms contain $\sqrt{3}$, we can add the coefficients:
$$ (9.4 + 4)\sqrt{3} = 13.4\sqrt{3} $$
-
Final expression
The final simplified expression is:
$$ 13.4\sqrt{3} $$
The simplified expression is $13.4\sqrt{3}$.
More Information
This result combines the coefficients of the like terms involving the square root of 3, showcasing an essential technique in simplifying expressions with square roots. Remember to always simplify square roots where possible to combine terms effectively.
Tips
- Neglecting root simplification: Failing to simplify square roots can lead to incorrect combinations of terms.
- Incorrect addition of coefficients: Carelessly adding coefficients without ensuring they are like terms results in mistakes.
AI-generated content may contain errors. Please verify critical information