(8y^3)(-3x^2y^2)(3/8 xy^4)
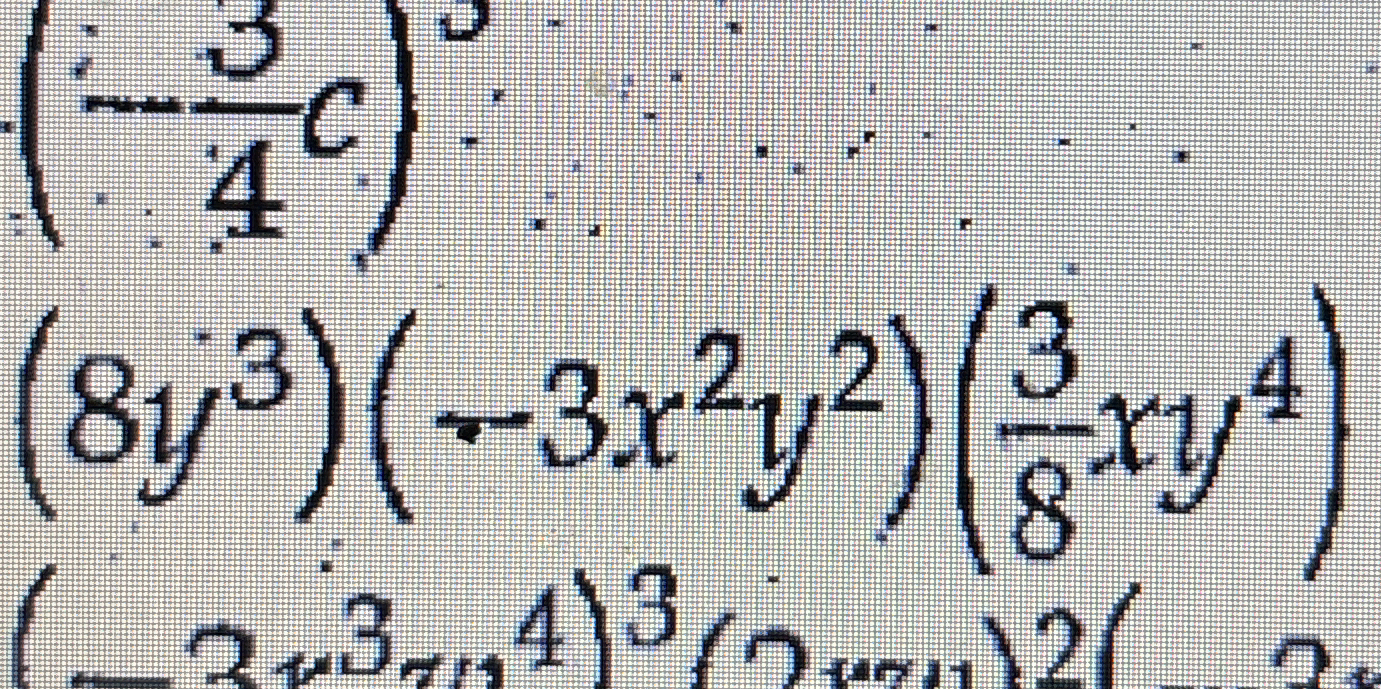
Understand the Problem
The question involves a mathematical expression with variables and coefficients that are to be manipulated or simplified. It seems to involve multiplication and possibly simplification of algebraic terms.
Answer
The final result is $$ -9x^3y^9 $$
Answer for screen readers
The final answer is
$$ -9x^3y^9 $$
Steps to Solve
- Multiply the coefficients We start by multiplying the coefficients of the terms. The coefficients are (8), (-3), and (\frac{3}{8}).
[ 8 \times (-3) \times \frac{3}{8} = -9 ]
- Combine the (x) terms Next, we multiply the (x) terms from each expression: (x^0) (from the first term), (x^2) (from the second term), and (x^1) (from the third term).
[ x^{0 + 2 + 1} = x^3 ]
- Combine the (y) terms Now, we multiply the (y) terms: (y^3) (from the first term), (y^2) (from the second term), and (y^4) (from the third term).
[ y^{3 + 2 + 4} = y^9 ]
- Combine all parts Now, we combine everything together into a single expression:
[ -9x^3y^9 ]
The final answer is
$$ -9x^3y^9 $$
More Information
This expression represents the result of multiplying the three given algebraic expressions together. The negative sign indicates that the result is a negative value, while the terms (x^3) and (y^9) denote the powers of the variables in the final expression.
Tips
- Forgetting to handle negative signs: Students may forget to properly account for the negative coefficient in the second term.
- Incorrectly adding exponents: When combining like terms, it's important to remember to add exponents only for terms with the same base.
AI-generated content may contain errors. Please verify critical information