∫(8/x - 5/x^2 + 6/x^3)dx
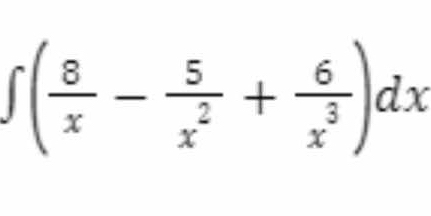
Understand the Problem
The question is asking for the indefinite integral of a function involving fractions and powers of x. We will solve it by integrating each term separately.
Answer
$$ 8 \ln |x| + \frac{5}{x} - \frac{3}{x^2} + C $$
Answer for screen readers
$$ 8 \ln |x| + \frac{5}{x} - \frac{3}{x^2} + C $$
Steps to Solve
- Separate the Terms for Integration
We can integrate each term of the function separately. The integral can be written as: $$ \int \left(\frac{8}{x} - \frac{5}{x^2} + \frac{6}{x^3}\right) dx = \int \frac{8}{x} , dx - \int \frac{5}{x^2} , dx + \int \frac{6}{x^3} , dx $$
- Integrate the First Term
The integral of ( \frac{8}{x} ) is: $$ \int \frac{8}{x} , dx = 8 \ln |x| $$
- Integrate the Second Term
For the second term, ( -\frac{5}{x^2} ), we rewrite it as ( -5x^{-2} ): $$ \int -\frac{5}{x^2} , dx = -5 \int x^{-2} , dx = -5 \left(-\frac{1}{x}\right) = \frac{5}{x} $$
- Integrate the Third Term
Similarly, for the third term ( \frac{6}{x^3} ), rewrite as ( 6x^{-3} ): $$ \int \frac{6}{x^3} , dx = 6 \int x^{-3} , dx = 6 \left(-\frac{1}{2x^2}\right) = -\frac{3}{x^2} $$
- Combine the Results
Now, we combine the results of the integrals: $$ 8 \ln |x| + \frac{5}{x} - \frac{3}{x^2} + C $$
where ( C ) is the constant of integration.
$$ 8 \ln |x| + \frac{5}{x} - \frac{3}{x^2} + C $$
More Information
The result combines logarithmic and rational functions, showcasing the process of integrating functions involving fractions and powers. The constant of integration (( C )) accounts for the family of antiderivatives.
Tips
- Forgetting to include the absolute value in ( \ln |x| ).
- Incorrectly applying the integration formula for powers, particularly negative powers.
