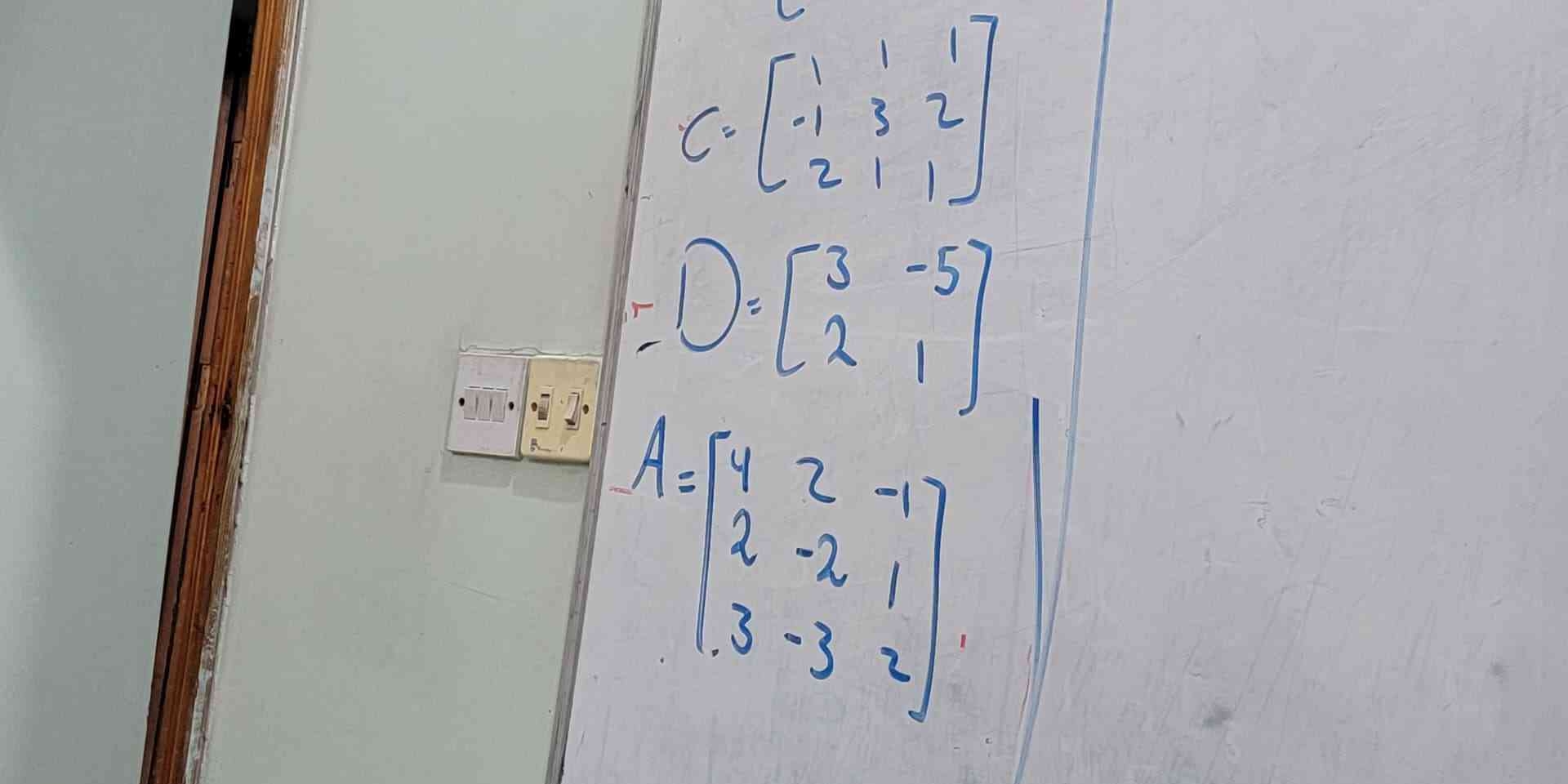
Understand the Problem
The question involves a mathematical scenario pertaining to matrices, likely dealing with operations such as addition, subtraction, or multiplication involving matrices A, B, C, and D. The user may need assistance in calculating the result or a specific operation involving these matrices.
Answer
The product of matrices $C$ and $D$ is $$ E = \begin{bmatrix} 5 & -4 \\ 3 & 8 \\ 8 & -9 \end{bmatrix} $$
Answer for screen readers
The product of matrices $C$ and $D$ is
$$ E = \begin{bmatrix} 5 & -4 \ 3 & 8 \ 8 & -9 \end{bmatrix} $$
Steps to Solve
-
Identify Matrix Dimensions Matrix $C$ is a $3 \times 3$ matrix, while Matrix $D$ is a $3 \times 2$ matrix. Matrix $A$ is also a $3 \times 3$ matrix.
-
Determine Compatibility for Multiplication To multiply matrices, the number of columns in the first matrix must equal the number of rows in the second matrix. Here, we can multiply $C$ ($3 \times 3$) with $D$ ($3 \times 2$) since the number of columns in $C$ (3) matches the number of rows in $D$ (2).
-
Matrix Multiplication of C and D The product of matrices $C$ and $D$ will form a new matrix $E$. The resulting matrix will have dimensions of $3 \times 2$.
Calculating each element of matrix $E$:
[ E_{ij} = \sum_{k=1}^{n} C_{ik} D_{kj} ]
For example, the element $E_{11}$ (first row, first column) is calculated as:
[ E_{11} = C_{11}D_{11} + C_{12}D_{21} = 1 \cdot 3 + 1 \cdot 2 = 5 ]
Continue calculating the remaining elements of $E$:
-
For $E_{12}$: [ E_{12} = C_{11}D_{12} + C_{12}D_{22} = 1 \cdot -5 + 1 \cdot 1 = -4 ]
-
For $E_{21}$: [ E_{21} = C_{21}D_{11} + C_{22}D_{21} = -1 \cdot 3 + 3 \cdot 2 = 3 ]
-
For $E_{22}$: [ E_{22} = C_{21}D_{12} + C_{22}D_{22} = -1 \cdot -5 + 3 \cdot 1 = 8 ]
-
For $E_{31}$: [ E_{31} = C_{31}D_{11} + C_{32}D_{21} = 2 \cdot 3 + 1 \cdot 2 = 8 ]
-
For $E_{32}$: [ E_{32} = C_{31}D_{12} + C_{32}D_{22} = 2 \cdot -5 + 1 \cdot 1 = -9 ]
- Construct Resulting Matrix E Now we can write matrix $E$:
[ E = \begin{bmatrix} 5 & -4 \ 3 & 8 \ 8 & -9 \end{bmatrix} ]
- Matrix A and B Calculation (If Needed) If we need to perform operations with matrix $A$, ensure to check the dimensions first for compatibility for further operations.
The product of matrices $C$ and $D$ is
$$ E = \begin{bmatrix} 5 & -4 \ 3 & 8 \ 8 & -9 \end{bmatrix} $$
More Information
Matrix multiplication combines the rows of the first matrix with the columns of the second. This operation is fundamental in linear algebra and has applications in various fields like computer graphics, statistics, and machine learning.
Tips
- Mixing up the order of multiplication; remember that matrix multiplication is not commutative.
- Failing to ensure that the inner dimensions match when multiplying matrices.
AI-generated content may contain errors. Please verify critical information