729 - 512x³y³, express in factored form.
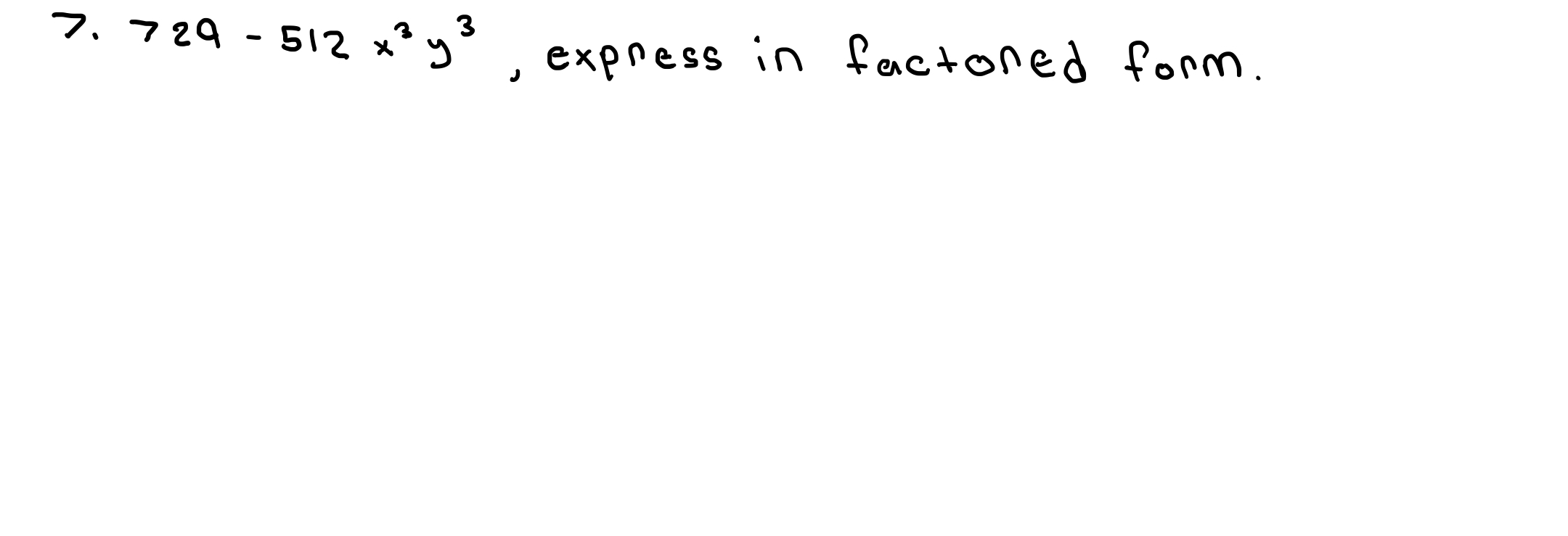
Understand the Problem
The question is asking to factor the expression 729 - 512x³y³. This involves recognizing and applying factoring techniques, likely factoring the expression as a difference of cubes.
Answer
The factored form of the expression is $$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$.
Answer for screen readers
The factored form of $729 - 512x^3y^3$ is:
$$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$
Steps to Solve
-
Identify the difference of cubes
The expression $729 - 512x^3y^3$ can be recognized as a difference of cubes since $729 = 9^3$ and $512x^3y^3 = (8xy)^3$. -
Apply the difference of cubes formula
The difference of cubes can be factored using the formula:
$$ a^3 - b^3 = (a - b)(a^2 + ab + b^2) $$
In this case, let $a = 9$ and $b = 8xy$. -
Substitute into the formula
Now substitute $a$ and $b$:
$$ (9 - 8xy)(9^2 + 9(8xy) + (8xy)^2) $$ -
Calculate the components
Now calculate each part:
- First term: $9 - 8xy$ is already factored.
- Second term:
- Calculate $9^2 = 81$
- Calculate $9(8xy) = 72xy$
- Calculate $(8xy)^2 = 64x^2y^2$
So the second term becomes: $81 + 72xy + 64x^2y^2$.
- Combine for the final factored form
Putting it all together:
$$ 729 - 512x^3y^3 = (9 - 8xy)(81 + 72xy + 64x^2y^2) $$
The factored form of $729 - 512x^3y^3$ is:
$$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$
More Information
The expression is factored using the difference of cubes method, which is a powerful technique in algebra for simplifying polynomial expressions. Recognizing cubes is key to applying this technique effectively.
Tips
- Forgetting the cube roots: Make sure to correctly identify the numbers being cubed.
- Misapplying the formula: Be careful with the signs and order of terms in the difference of cubes formula.
AI-generated content may contain errors. Please verify critical information