729 - 512x^3y^3, express in factored form.
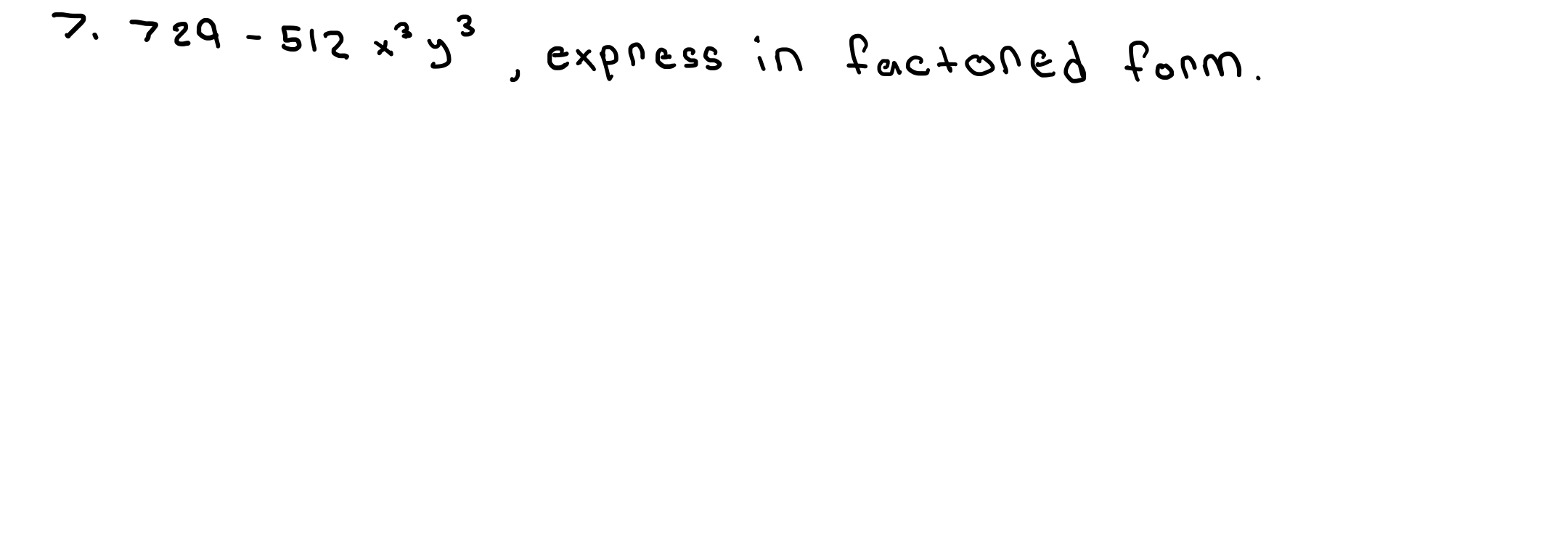
Understand the Problem
The question is asking to express the polynomial 729 - 512x^3y^3 in factored form. This involves identifying common factors or using techniques such as factoring the difference of cubes.
Answer
$$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$
Answer for screen readers
The factored form of the polynomial $729 - 512x^3y^3$ is:
$$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$
Steps to Solve
-
Identify the difference of cubes
Recognize that the expression $729 - 512x^3y^3$ can be seen as a difference of cubes. We can rewrite the constants:
$$729 = 9^3$$
$$512x^3y^3 = (8xy)^3$$
Thus, the expression becomes:
$$9^3 - (8xy)^3$$ -
Apply the difference of cubes formula
The difference of cubes can be factored using the formula:
$$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$$
Here, we let $a = 9$ and $b = 8xy$. Now we can apply the formula:
$$9^3 - (8xy)^3 = (9 - 8xy)(9^2 + 9 \cdot 8xy + (8xy)^2)$$ -
Calculate the components
First, calculate each part of the factorization:
- The first factor simplifies to:
$$9 - 8xy$$ - The second factor simplifies as follows:
$$9^2 = 81$$
$$9 \cdot 8xy = 72xy$$
$$(8xy)^2 = 64x^2y^2$$
Putting these together:
$$81 + 72xy + 64x^2y^2$$
- Combine the factors
So, the factored form of the polynomial is:
$$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$
The factored form of the polynomial $729 - 512x^3y^3$ is:
$$(9 - 8xy)(81 + 72xy + 64x^2y^2)$$
More Information
This factored form showcases the use of the difference of cubes, a key algebraic concept, which allows us to express a polynomial in a simpler multiplicative form. Recognizing patterns in polynomials, such as cubes, can simplify complex problems.
Tips
One common mistake is miscalculating the components of the difference of cubes. To avoid this, always ensure you accurately compute $a^2$, $ab$, and $b^2$ based on the correct values for $a$ and $b$.
AI-generated content may contain errors. Please verify critical information