√72 - 4√8 + √200
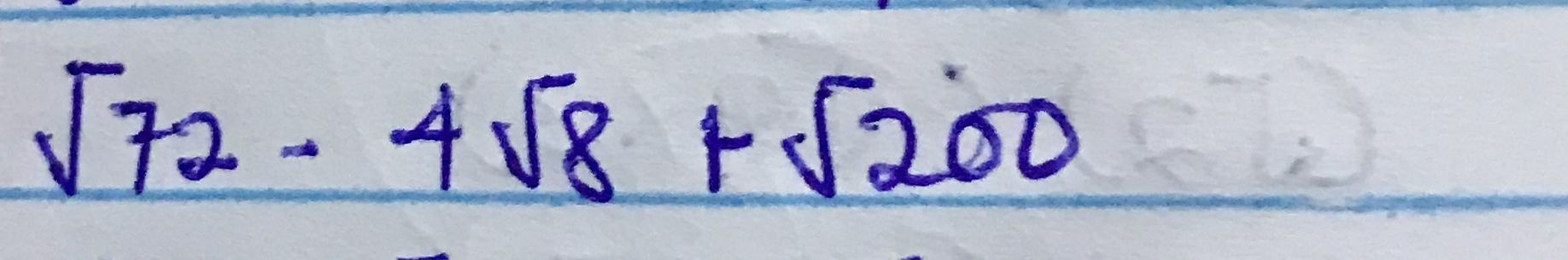
Understand the Problem
The question is asking to simplify the expression involving square roots: √72 - 4√8 + √200. This involves rewriting the square roots in a more manageable form and performing arithmetic operations.
Answer
The simplified expression is $8\sqrt{2}$.
Answer for screen readers
The final simplified expression is $8\sqrt{2}$.
Steps to Solve
- Simplify √72
To simplify $\sqrt{72}$, we can factor it as follows:
$$\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}$$
- Simplify -4√8
Next, we simplify $-4\sqrt{8}$:
$$-4\sqrt{8} = -4\sqrt{4 \cdot 2} = -4\sqrt{4} \cdot \sqrt{2} = -4 \cdot 2\sqrt{2} = -8\sqrt{2}$$
- Simplify √200
Now, we simplify $\sqrt{200}$:
$$\sqrt{200} = \sqrt{100 \cdot 2} = \sqrt{100} \cdot \sqrt{2} = 10\sqrt{2}$$
- Combine all the simplified terms
We can now combine all the terms:
$$6\sqrt{2} - 8\sqrt{2} + 10\sqrt{2}$$
This can be simplified by combining like terms:
$$ (6 - 8 + 10)\sqrt{2} = 8\sqrt{2} $$
The final simplified expression is $8\sqrt{2}$.
More Information
The expression was simplified by breaking down the square roots into manageable parts and combining like terms. The process illustrates the importance of recognizing perfect squares within the square roots.
Tips
- A common mistake is forgetting to factor out perfect squares correctly, leading to incorrect simplifications.
- Another mistake is failing to combine like terms once the expressions have been simplified.
AI-generated content may contain errors. Please verify critical information