Understand the Problem
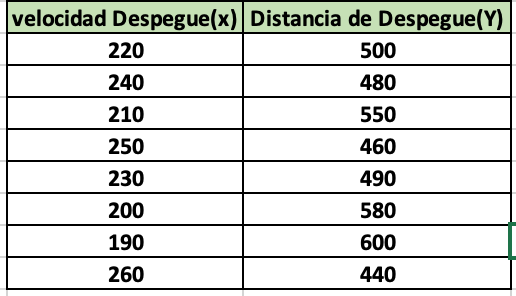
La pregunta parece estar relacionada con una tabla que presenta datos sobre la velocidad de despegue y la distancia de despegue. Es probable que se deba realizar algún tipo de análisis de estos datos, como graficar la relación o calcular alguna tendencia.
Answer
La ecuación de la recta es $Y = mx + b$.
Answer for screen readers
La ecuación de la recta de regresión es:
$$ Y = mx + b $$
donde se calculan los valores de $m$ y $b$ según los pasos anteriores.
Steps to Solve
-
Organizar los datos
La tabla proporciona dos conjuntos de datos: velocidad de despegue (x) y distancia de despegue (Y). Los datos son:
(220, 500) (240, 480) (210, 550) (250, 460) (230, 490) (200, 580) (190, 600) (260, 440) -
Calcular la media de x y Y
Para encontrar las medias de ambos conjuntos de datos, se utiliza la fórmula:
- Media de X:
$$ \bar{x} = \frac{\sum x_i}{n} $$
- Media de Y:
$$ \bar{y} = \frac{\sum y_i}{n} $$
Donde $n$ es el número de observaciones.
-
Calcular la covarianza
La covarianza se calcula para entender la relación entre x y Y usando la fórmula:
$$ \text{Cov}(X,Y) = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{n} $$
-
Calcular la varianza de x
La varianza de X se obtiene de la siguiente manera:
$$ \text{Var}(X) = \frac{\sum (x_i - \bar{x})^2}{n} $$
-
Calcular la pendiente (m) de la regresión lineal
Usando la covarianza y la varianza, se determina la pendiente (m) de la recta de regresión lineal:
$$ m = \frac{\text{Cov}(X,Y)}{\text{Var}(X)} $$
-
Calcular la intersección (b) de la regresión
Una vez obtenida la pendiente, la intersección (b) se calcula con:
$$ b = \bar{y} - m\bar{x} $$
-
Formar la ecuación de la recta de regresión
La ecuación de la recta de regresión se expresa como:
$$ Y = mx + b $$
-
Interpretar los resultados
Se analiza qué significa la pendiente y la intersección respecto a la relación entre velocidad de despegue y distancia de despegue.
La ecuación de la recta de regresión es:
$$ Y = mx + b $$
donde se calculan los valores de $m$ y $b$ según los pasos anteriores.
More Information
Esta ecuación permite predecir la distancia de despegue basándose en la velocidad de despegue. Los resultados pueden ser utilizados en aviación para optimizar despegues.
Tips
- No restar las medias en los cálculos de covarianza.
- Olvidar sumar los términos antes de dividir por n.
- Cometer errores de cálculo al encontrar la pendiente y la intersección.
AI-generated content may contain errors. Please verify critical information