6√5 - 2√5 + 8√5
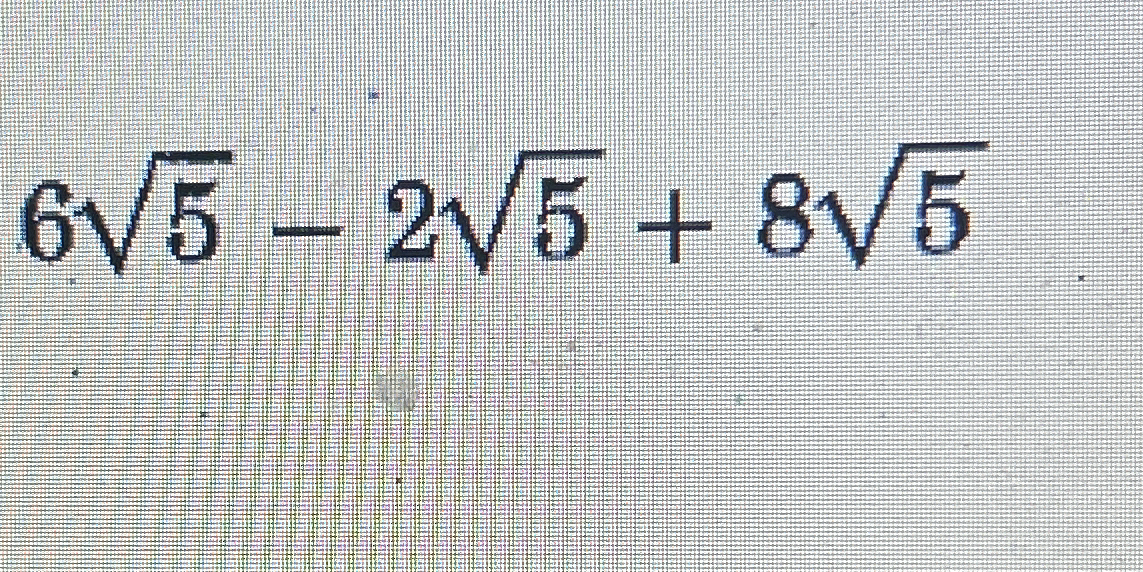
Understand the Problem
The question is asking to simplify the expression involving square roots. The expression consists of multiple terms that can be combined based on their coefficients of the square root of 5.
Answer
The simplified expression is \( 12\sqrt{5} \).
Answer for screen readers
The simplified expression is ( 12\sqrt{5} ).
Steps to Solve
- Identify the Similar Terms
First, look at the expression: ( 6\sqrt{5} - 2\sqrt{5} + 8\sqrt{5} ). All terms involve ( \sqrt{5} ), which means they can be combined.
- Combine the Coefficients
Next, combine the coefficients of ( \sqrt{5} ):
$$ 6 - 2 + 8 $$
- Calculate the Sum
Now, perform the arithmetic:
- Subtract ( 2 ) from ( 6 ): $$ 6 - 2 = 4 $$
- Then add ( 8 ): $$ 4 + 8 = 12 $$
- Write the Final Expression
So, the combined expression becomes:
$$ 12\sqrt{5} $$
The simplified expression is ( 12\sqrt{5} ).
More Information
The expression ( 12\sqrt{5} ) represents a simplified form of the original expression, making it easier to work with in further calculations. Combining similar terms is a crucial skill in algebra.
Tips
- A common mistake is forgetting to combine all coefficients correctly or not recognizing that terms involving the same square root can be combined.
- Another mistake is miscalculating the arithmetic when combining the coefficients.
AI-generated content may contain errors. Please verify critical information