6. For the function f(x) in the graph below, determine the following: a. $\lim_{x \to -2^{-}} f(x)$ b. $\lim_{x \to 2^{-}} f(x)$ c. $\lim_{x \to 2^{+}} f(x)$ d. f(2) 7. Use the gr... 6. For the function f(x) in the graph below, determine the following: a. $\lim_{x \to -2^{-}} f(x)$ b. $\lim_{x \to 2^{-}} f(x)$ c. $\lim_{x \to 2^{+}} f(x)$ d. f(2) 7. Use the graph to find the limit, if it exists. a. $\lim_{x \to -2} f(x)$ b. $\lim_{x \to 2} f(x)$ c. $\lim_{x \to 3} f(x)$
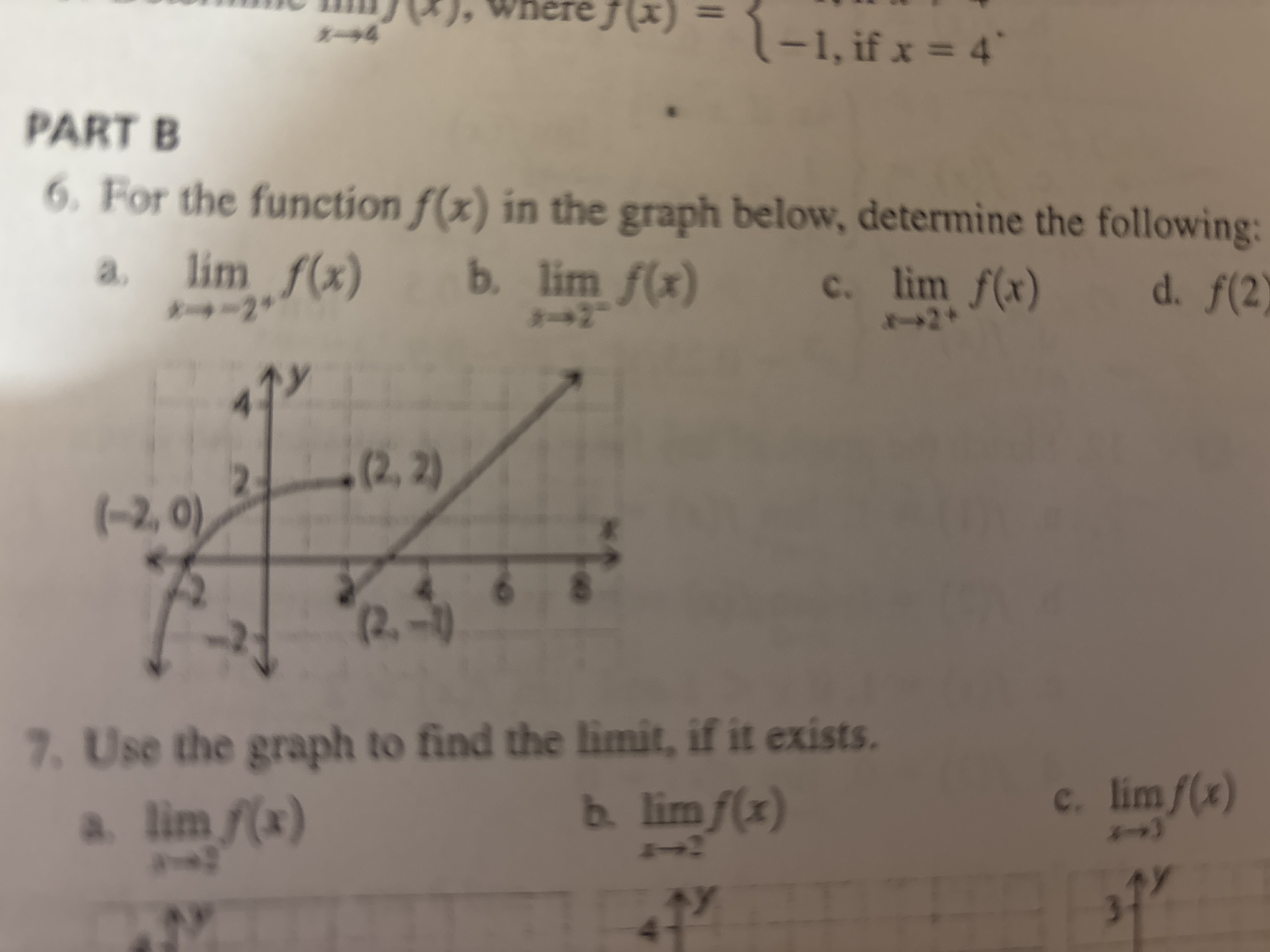
Understand the Problem
The question is asking us to determine the limits and function values based on the graphs provided. For question 6, we need to find the left-hand limit as x approaches -2, the left and right hand limits as x approaches 2, and evaluate the function at x = 2. For question 7, we need to use the graphs to find the limits as x approaches -2, 2, and 3, if they exist.
Answer
6. a. $\lim_{x \to -2^-} f(x) = 0$ b. $\lim_{x \to 2^-} f(x) = 2$ c. $\lim_{x \to 2^+} f(x) = -1$ d. $f(2) = 2$ 7. a. $\lim_{x \to -2} f(x) = 0$ b. $\lim_{x \to 2} f(x)$ does not exist. c. $\lim_{x \to 3} f(x) = 2$
Answer for screen readers
a. $\lim_{x \to -2^-} f(x) = 0$ b. $\lim_{x \to 2^-} f(x) = 2$ c. $\lim_{x \to 2^+} f(x) = -1$ d. $f(2) = 2$
a. $\lim_{x \to -2} f(x) = 0$ b. $\lim_{x \to 2} f(x)$ does not exist. c. $\lim_{x \to 3} f(x) = 2$
Steps to Solve
-
6a: Find the left-hand limit as x approaches -2
From the graph, as $x$ approaches $-2$ from the left (i.e., $x \to -2^-$), the function $f(x)$ approaches $0$.
-
6b: Find the left-hand limit as x approaches 2
From the graph, as $x$ approaches $2$ from the left (i.e., $x \to 2^-$), the function $f(x)$ approaches $2$.
-
6c: Find the right-hand limit as x approaches 2
From the graph, as $x$ approaches $2$ from the right (i.e., $x \to 2^+$), the function $f(x)$ approaches $-1$.
-
6d: Find the function value at x = 2
From the graph, the value of the function at $x = 2$ is $f(2) = 2$.
-
7a: Find the limit as x approaches -2
From the graph, as $x$ approaches $-2$ from the right (i.e., $x \to -2^+$), the function $f(x)$ approaches $0$. So $\lim_{x \to -2} f(x) = 0$.
-
7b: Find the limit as x approaches 2
Since the left-hand limit and the right-hand limit at $x=2$ are not equal ($\lim_{x \to 2^-} f(x) = 2$ and $\lim_{x \to 2^+} f(x) = -1$), the limit as $x$ approaches $2$ does not exist.
-
7c: Find the limit as x approaches 3
From the graph, as $x$ approaches $3$, the function $f(x)$ approaches $2$. Therefore, $\lim_{x \to 3} f(x) = 2$.
a. $\lim_{x \to -2^-} f(x) = 0$ b. $\lim_{x \to 2^-} f(x) = 2$ c. $\lim_{x \to 2^+} f(x) = -1$ d. $f(2) = 2$
a. $\lim_{x \to -2} f(x) = 0$ b. $\lim_{x \to 2} f(x)$ does not exist. c. $\lim_{x \to 3} f(x) = 2$
More Information
Limits describe the behavior of a function as it approaches a particular $x$ value, while the function value is the actual output of the function at that $x$ value. One-sided limits consider the function's behavior approaching from either the left or right. For a limit to exist, the left-hand and right-hand limits must be equal.
Tips
A common mistake is confusing the limit of a function as $x$ approaches a value with the actual value of the function at that point. These can be different, especially for piecewise functions or functions with discontinuities. Another common mistake is assuming that if a function is defined at a point, the limit at that point always exists or equals the function's value.
AI-generated content may contain errors. Please verify critical information