5m^{-1} / 9(ab)^{-4} c^{7}
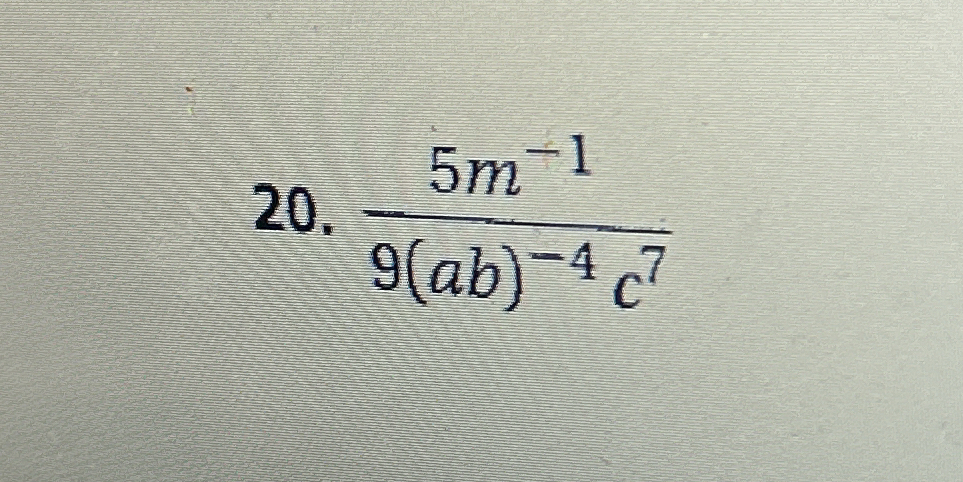
Understand the Problem
The question presents a mathematical expression involving variables and exponents, likely asking for simplification or evaluation as part of a homework problem.
Answer
The simplified expression is $$ \frac{5(ab)^4}{9mc^7} $$
Answer for screen readers
The simplified expression is
$$ \frac{5(ab)^4}{9mc^7} $$
Steps to Solve
- Write out the expression clearly
The original expression is
$$ \frac{5m^{-1}}{9(ab)^{-4}c^{7}} $$
- Simplify the expression
To simplify, we will handle the negative exponents. Recall that $x^{-n} = \frac{1}{x^n}$. This means:
- $m^{-1} = \frac{1}{m}$
- $(ab)^{-4} = \frac{1}{(ab)^4}$
Substituting in, we have:
$$ \frac{5}{m} \cdot \frac{1}{9 \cdot \frac{1}{(ab)^4} \cdot c^7} $$
This simplifies to:
$$ \frac{5 \cdot (ab)^4}{9c^7} \cdot \frac{1}{m} $$
- Combine the factors
Now combine all parts together:
$$ \frac{5 \cdot (ab)^4}{9m \cdot c^7} $$
- Final expression
Thus, the final simplified version of the original expression is:
$$ \frac{5(ab)^4}{9mc^7} $$
The simplified expression is
$$ \frac{5(ab)^4}{9mc^7} $$
More Information
This simplification helps clarify how to handle negative exponents, turning them into fractions. It's a fundamental part of working with algebraic expressions, especially when dealing with variables and exponents.
Tips
- Ignoring negative exponents: Remember that a negative exponent means the term should be in the denominator.
- Misplacing brackets: Ensure parentheses are correctly used, especially when dealing with products of variables.
- Forgetting to simplify completely: Always check if the final expression can be further reduced.
AI-generated content may contain errors. Please verify critical information