∫ -5cos(πx) dx
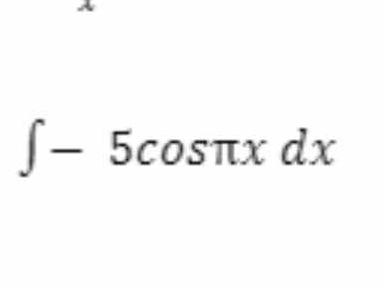
Understand the Problem
The question involves calculating the integral of the function -5cos(πx) with respect to x. The goal is to find the indefinite integral and express it in a simplified form.
Answer
The indefinite integral is $-\frac{5}{\pi} \sin(\pi x) + C$.
Answer for screen readers
The indefinite integral is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
Steps to Solve
-
Identify the integral We start with the integral ( \int -5 \cos(\pi x) , dx ).
-
Factor out the constant Since (-5) is a constant, we can factor it out of the integral: $$ \int -5 \cos(\pi x) , dx = -5 \int \cos(\pi x) , dx $$
-
Integral of cosine function The integral of (\cos(kx)) is (\frac{1}{k} \sin(kx)). In our case, (k = \pi): $$ \int \cos(\pi x) , dx = \frac{1}{\pi} \sin(\pi x) + C $$ where (C) is the constant of integration.
-
Combine the results Now we combine this with the factor of (-5): $$ -5 \int \cos(\pi x) , dx = -5 \left( \frac{1}{\pi} \sin(\pi x) + C \right) $$
-
Final answer Distributing the (-5): $$ -5 \cdot \frac{1}{\pi} \sin(\pi x) - 5C = -\frac{5}{\pi} \sin(\pi x) + C' $$ where (C' = -5C) is just another constant.
The indefinite integral is: $$ -\frac{5}{\pi} \sin(\pi x) + C $$
More Information
This integral represents the area under the curve of the function (-5 \cos(\pi x)) over a range of (x). The factor (-\frac{5}{\pi}) modifies the sinusoidal function, affecting its amplitude.
Tips
- Forgetting to include the constant of integration: Always remember to add (C) to the result of indefinite integrals.
- Misapplying the integral of cosine: Ensure proper understanding of the formula, especially with the (k) values.
