5a^4 x 3a^2 ÷ a^-3
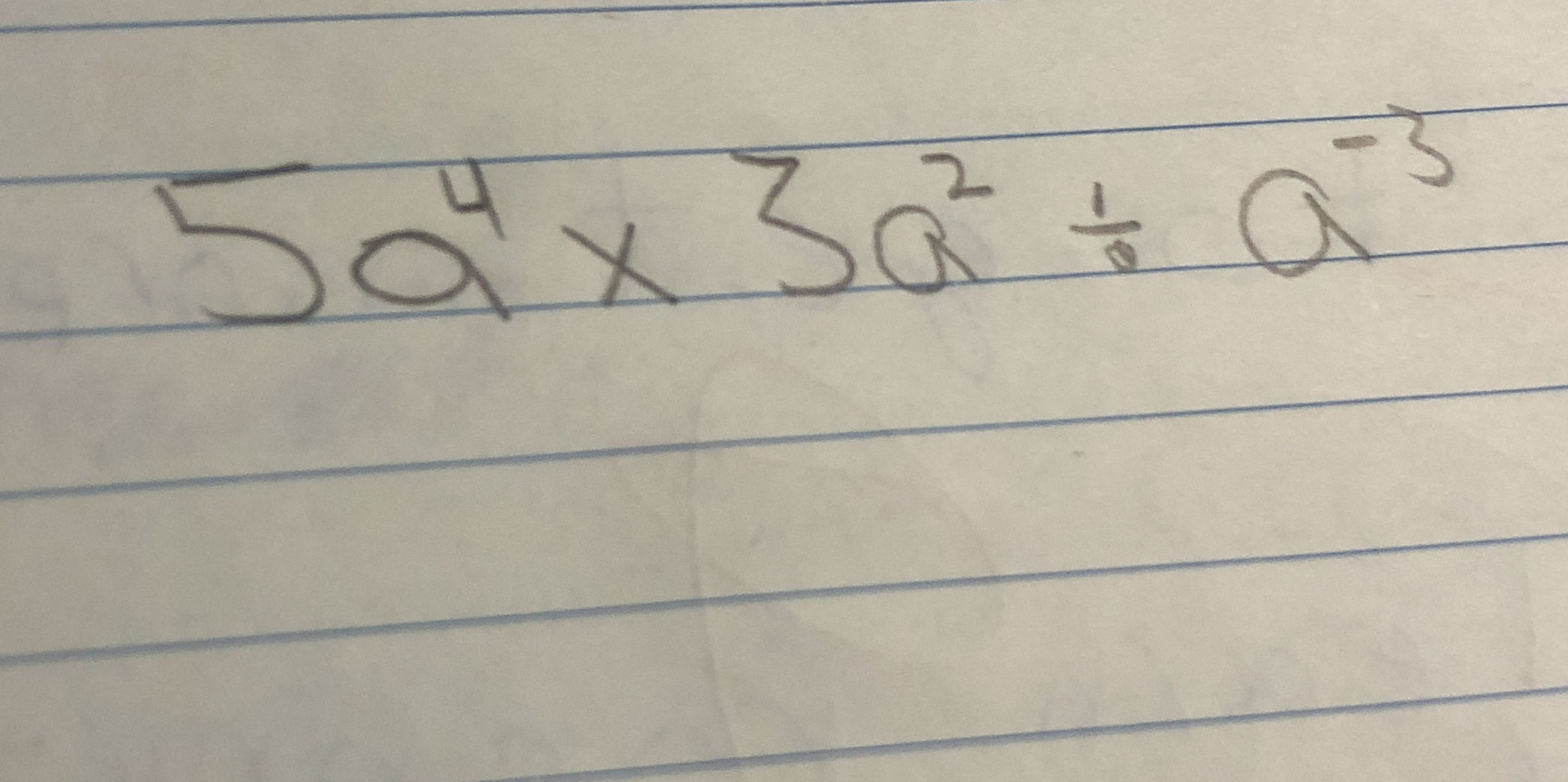
Understand the Problem
The question is asking to simplify the expression involving algebraic terms, specifically focusing on the multiplication and division of powers with the variables present.
Answer
The simplified expression is \(15a^{9}\).
Answer for screen readers
The simplified expression is (15a^{9}).
Steps to Solve
-
Identify the Terms The expression to simplify is (5a^4 \times 3a^2 \div a^{-3}).
-
Multiply the Constants and Add the Exponents First, multiply the constants: $$ 5 \times 3 = 15 $$
Next, add the exponents of (a) in (5a^4 \times 3a^2): $$ a^4 \times a^2 = a^{4+2} = a^{6} $$
So we have: $$ 15a^6 $$
- Apply Division of Powers Now, divide (15a^6) by (a^{-3}). When dividing powers, we subtract the exponents: $$ a^6 \div a^{-3} = a^{6 - (-3)} = a^{6 + 3} = a^{9} $$
Combining these gives: $$ 15a^{9} $$
The simplified expression is (15a^{9}).
More Information
This expression combines the multiplication of coefficients and the properties of exponents. The fundamental rules used include multiplying coefficients and adding exponents during multiplication, and subtracting exponents during division.
Tips
- Forgetting to apply the negative exponent rule correctly (subtracting instead of adding when dividing).
- Ignoring the multiplication of coefficients which can lead to incorrect answers.
AI-generated content may contain errors. Please verify critical information